NumPy矩阵运算：矩阵降维（主成分分析法）
- NumPy矩阵运算
- 19小时前
- 24热度
- 0评论
数据降维
数据降维就是把一堆原本很复杂、维度很高的数据，通过某种方法变成更简单、维度更低的数据，同时尽量保留原数据的重要信息和特征。这就像是你在整理一堆杂乱的书籍或文件时，可能会把它们按照不同的主题或类别进行分类和归纳，这样虽然你手上的东西还是那么多，但是看起来更清晰、更容易管理。
在数据处理中，数据可能包含了很多维度（比如，一个人的信息可能包括年龄、性别、身高、体重、收入、职业等多个维度），处理这些数据会很复杂、很耗时，若这些维度之间存在一些关联或冗余，就可以尝试通过降维来减少这种复杂性。
举个例子，假设你正在分析一群人的健康数据，数据里有他们的身高、体重、腰围、臀围等多个指标。你发现“体重”和“身高”这两个维度已经能够很好地反映一个人的体型特征，而“腰围”和“臀围”虽然也是有用的信息，但在某种程度上与“体重”和“身高”是有关联的。那么，在不影响分析结果的情况下，可以考虑只保留“身高”和“体重”这两个维度，这样数据的处理就会变得更加简单和高效。
主成分分析法(PCA)
主成分分析法(PCA)在数据降维领域应用的最为广泛，它是一种无监督学习方法，其主要观点是认为数据的特征属性之间存在线性相关，导致数据间的信息冗余，通过正交变换把线性相关的特征用较少线性无关的数据来表示，以达到降维的目的。
假设存在下面的矩阵：
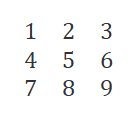
当前矩阵是三维矩阵，希望将矩阵降维到1维，且不改变该矩阵的主要特征。实现PCA降维的基本步骤如下图所示。
数据标准化
对矩阵进行标准化处理（也称为归一化或Z-score标准化），目的是使得矩阵中的每个特征（列）都拥有相同的尺度，即均值为0，标准差为1。这样的处理在机器学习和数据预处理中非常常见，因为它有助于改善很多算法的性能，特别是那些对特征尺度敏感的算法。
python代码示例：
import numpy as np
def standardize_matrix(matrix):
"""
对矩阵进行标准化处理，使得每列（特征）的均值为0，标准差为1。
参数:
- matrix: numpy数组，其中每一列代表一个特征，每一行代表一个样本。
返回:
- standardized_matrix: 标准化后的numpy数组。
"""
# 计算每列的均值
mean_vals = np.mean(matrix, axis=0)
# 计算每列的标准差
std_vals = np.std(matrix, axis=0, ddof=1) # 使用样本标准差（ddof=1）
# 防止除以0的情况
std_vals[std_vals == 0] = 1
# 标准化矩阵
standardized_matrix = (matrix - mean_vals) / std_vals
return standardized_matrix
# 示例使用
if __name__ == "__main__":
# 假设我们有一个如下的矩阵
matrix = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
# 标准化矩阵
standardized_matrix = standardize_matrix(matrix)
# 打印结果
print("原始矩阵:")
print(matrix)
print("标准化后的矩阵:")
print(standardized_matrix)
示例代码首先计算了输入矩阵matrix每列的均值和标准差，然后使用这些统计量对矩阵进行了标准化处理。运行这段代码，你会看到原始矩阵和标准化后的矩阵的输出，其中标准化后的矩阵的每列均值接近0，标准差接近1（由于数值精度，可能不会完全精确）。
计算协方差矩阵
降维的目的就是降噪和去冗余。降噪就是使保留下来的维度间的相关性尽可能小，去冗余就是使保留下来的维度含有的方差尽可能大，因此需要知道各维度间的相关性以及个维度上的方差。
协方差矩阵能够表现不同维度间的相关性以及各个维度上的方差， 它度量的是维度与维度之间的关系，而非样本与样本之间，其主对角线上的元素是各个维度上的方差，其他元素是两两维度间的协方差。
我们要的东西协方差矩阵都有了，先来看降噪，让保留下的不同维度间的相关性尽可能小，也就是说让协方差矩阵中非对角线元素都基本为零。对角化后的协方差矩阵。再看去冗余，对角线上较小的新方差对应的就是那些该去掉的维度，只取那些含有较大特征值的维度，其余的就舍掉即可。
python代码示例：
import numpy as np
def calculate_covariance_matrix(data):
"""
计算给定数据集的协方差矩阵。
参数:
- data: numpy数组，其中每一列代表一个特征，每一行代表一个观测值（样本）。
返回:
- covariance_matrix: 协方差矩阵的numpy数组。
"""
# 计算协方差矩阵
covariance_matrix = np.cov(data, rowvar=False)
return covariance_matrix
# 示例使用
if __name__ == "__main__":
# 假设我们有一个如下的数据集
data = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 10]
])
# 计算协方差矩阵
covariance_matrix = calculate_covariance_matrix(data)
# 打印结果
print("协方差矩阵:")
print(covariance_matrix)
在示例代码中，np.cov函数用于计算协方差矩阵。参数rowvar=False表示输入数组中的每一列代表一个变量（特征），每一行代表一个观测值（样本），这是最常见的用例。如果你的数据集是转置的（即，每一行代表一个变量），你应该将rowvar设置为True。
运行这段代码将输出数据集的协方差矩阵，其中包含了所有特征对之间的协方差值。对角线上的元素是每个特征的方差。
计算协方差矩阵的特征值和特征向量
得到协方差矩阵后，进一步获取协方差矩阵的特征向量和特征值。
# 计算协方差矩阵的特征值和特征向量
# covariance_matrix为计算后的协方差矩阵
eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)
选择主成分
根据特征值的大小选择最重要的特征向量（即主成分）。通常选择前k个特征向量，其中k小于原始特征的数量。
# 对特征值进行排序，并找到对应的特征向量
sorted_eigen_value_indices = np.argsort(eigenvalues)[::-1]
sorted_eigenvector_matrix = eigen_vectors[:, sorted_eigen_value_indices]
# 选择前k个特征向量
eigenvector_subset = sorted_eigenvector_matrix[:, 0:num_components]
数据转换
将原始数据投影到选定的主成分上，从而得到降维后的数据。
# 将数据转换到新的空间
X_reduced = np.dot(standardized_matrix, eigenvector_subset)
完整代码
python代码示例：
import numpy as np
def pca(X, num_components):
# 步骤1: 数据标准化
X_meaned = X - np.mean(X, axis=0)
# 步骤2: 计算协方差矩阵
cov_mat = np.cov(X_meaned, rowvar=False)
# 步骤3: 计算协方差矩阵的特征值和特征向量
eigen_values, eigen_vectors = np.linalg.eigh(cov_mat)
# 对特征值进行排序，并找到对应的特征向量
sorted_eigen_value_indices = np.argsort(eigen_values)[::-1]
sorted_eigenvector_matrix = eigen_vectors[:, sorted_eigen_value_indices]
# 步骤4: 选择前k个特征向量
eigenvector_subset = sorted_eigenvector_matrix[:, 0:num_components]
# 步骤5: 将数据转换到新的空间
X_reduced = np.dot(X_meaned, eigenvector_subset)
return X_reduced
# 示例数据
X = np.array([[1, 2], [3, 4], [5, 6]])
# 假设我们想将数据降到1维
num_components = 1
reduced_X = pca(X, num_components)
print("Reduced data:")
print(reduced_X)
实际应用中，数据标准化是非常重要的步骤，因为它确保了每个特征对结果的贡献是公平的。在选择主成分时，通常会根据特征值的大小来选择，特征值越大，对应的特征向量包含的信息就越多。
