机器学习算法基础：决策树回归算法

 

内容摘要

决策树回归算法的工作原理与猜数游戏非常相似。它通过对数据集进行一系列的划分，来构建一个树状结构。本文算法原理部分讲述了决策树的构建过程，应用案例部分通过建立波士顿房价预测模型，详细讨论了数据集的获取、导入、分割，构建决策树回归模型的详细工作过程，以及模型训练、评估和可视化方法。

 

理解决策树回归算法

‌决策树回归算法是一种用树的结构来预测数值的方法‌。

假设你正在玩一个猜数字的游戏，游戏的目标是猜出一个隐藏在背后的具体数值。为了更快地猜中这个数字，你可能会问一系列的问题，比如：“这个数字大于50吗？”“小于30呢？”“那是不是在40到50之间？”等等。通过这些问题，你可以一步步地缩小可能的数字范围，直到最终猜中那个数字。

决策树回归算法的工作原理与这个游戏非常相似。它通过对数据集进行一系列的划分，来构建一个树状结构。这个树状结构的每个内部节点都代表一个特征，每个分支代表一个判断结果的输出（比如“是”或“否”），而每个叶节点则代表一个预测值（最终猜中的那个数字，或在这个场景下，是一个平均值，用于预测落在该叶子节点对应区域内的样本的目标值）。

具体来说，决策树回归算法会遍历所有可能的特征和分裂点，选择能够最大程度减小预测误差（比如均方误差）的特征和分裂点作为最佳分裂。然后，它会继续对这些分裂后的子集进行递归划分，直到满足某个停止条件（比如达到最大深度、节点中样本数量小于阈值等）。最终，生成的决策树模型就可以用来对新的样本进行预测了。

算法原理

决策树的构建过程是一个自顶向下的递归过程，从根节点开始，通过选择最佳划分属性/特征来不断地将数据集划分为更小的子集，并为每个子集递归地构建子树。这个过程一直持续到满足某个停止条件为止，最终形成一个完整的决策树模型。

策树的构建过程主要包括以下几个步骤：

一、选择最佳划分属性/特征

‌目的‌：在决策树的每个节点上，需要找到一个能够最大化分类效果或最小化预测误差的属性/特征，作为当前节点的划分标准。

‌方法‌：对于分类问题，常用的指标包括信息增益、基尼系数等。信息增益衡量了使用某个特征进行划分后，数据集纯度（如熵或基尼不纯度）的减少量。基尼系数则反映了数据集中类别分布的均匀程度，基尼系数越小，表示数据集纯度越高。

对于回归问题，则通常使用最小化平方误差、绝对误差或其他相关损失函数来选择最佳划分特征。

‌实施‌：遍历所有可用的特征，计算每个特征作为划分标准时的指标值，然后选择指标最优的特征作为当前节点的划分属性。

二、划分数据集

‌依据‌：根据选择的最佳划分属性/特征，以及该属性/特征上的不同取值，将数据集划分为多个子集（也称为子节点或子树）。

‌结果‌：每个子集都包含了在该划分属性/特征上取值相同或相似的数据样本。

三、递归构建子树

‌过程‌：对于每个划分后得到的子集，都递归地执行上述两个步骤（选择最佳划分属性/特征和划分数据集），直到满足某个停止条件为止。

‌停止条件‌：

（1）达到预设的最大树深度。

（2）节点中的样本数量少于某个阈值，无法再进行有效的划分。

（3）划分后的子集纯度已经足够高（对于分类问题）或预测误差已经足够小（对于回归问题），进一步划分不再显著提高模型性能。

（4）其他自定义的停止条件，如达到最大迭代次数、最小信息增益等。

应用案例

一、案例目标

利用决策树回归算法，基于波士顿房价数据集，构建一个能够准确预测波士顿地区房屋价格的模型。波士顿房价数据集是一个著名的数据集，包含了506个样本，每个样本有13个特征变量和一个连续的目标变量（房屋价格中位数）。这些特征变量涵盖了城镇人均犯罪率、住宅用地所占比例、一氧化氮浓度、每栋住宅的房间数等多个方面。

本案例实现以下目标：

‌数据加载与预处理‌：使用sklearn库中的相关函数加载波士顿房价数据集，并对其进行必要的数据预处理，如划分训练集和测试集，以确保模型训练的有效性和可靠性。

‌决策树回归模型构建‌：基于决策树回归算法，构建一个能够拟合波士顿房价数据集的模型。我们将通过调整决策树模型的参数，如最大深度、节点分裂所需的最小样本数等，来优化模型的性能。

‌模型训练与评估‌：使用训练集对决策树回归模型进行训练，并使用测试集对模型的性能进行评估。通过计算预测结果的平均绝对误差、均方误差等指标，来衡量模型的预测准确性。

‌模型可视化与解释‌：使用sklearn库中的相关函数，将训练好的决策树回归模型进行可视化展示，以便直观地理解模型的决策过程。同时还将对模型的预测结果进行分析和解释，以验证模型的有效性和可靠性。

二、波士顿房价数据集

‌波士顿房价数据集是一个经典的用于回归分析的数据集，该数据集通过包含13个特征变量，描述了不同的社会经济和环境因素，如犯罪率、住宅用地比例、非零售商业用地比例、查尔斯河虚拟变量、一氧化氮浓度、每栋住宅的平均房间数、1940年之前建成的自用房屋比例等。房屋的中位数价格（MEDV），以千美元为单位，是数据集需要预测的目标。

特征变量详解‌

‌CRIM‌：城镇人均犯罪率，数值越高表示该地区犯罪率越高，通常会对房价产生负面影响。

‌ZN‌：25000平方英尺以上的住宅用地比例，反映了土地用途情况，可能与房价有一定关联。

‌INDUS‌：城镇非零售商业用地比例，体现了工商业发展程度对周边房价的潜在影响。

‌CHAS‌：查尔斯河虚拟变量，如果房屋靠近河流则值为1，否则为0。河流周边的房屋可能因景观等因素在价格上有差异。

‌NOX‌：一氧化氮浓度，是空气质量相关指标，也会影响居住舒适度及房价。

‌RM‌：每栋住宅的平均房间数，房间数量多可能意味着房屋面积更大，往往和房价正相关。

‌AGE‌：1940年之前建成的自用房屋比例，是房屋新旧程度的一种体现，老旧房屋比例高可能房价相对低些。

数据集包含506个样本，每个样本代表波士顿不同郊区的房屋信息。

三、导入数据集

在scikit-learn中，波士顿房价数据集通常作为一个内置的示例数据集提供。从scikit-learn 1.2版本开始，波士顿房价数据集被标记为弃用，因为它包含敏感和有偏见的特性。尽管如此，为了教学目的或在你确实了解数据集背景并接受其限制的情况下，你仍然可以导入和使用它。

如果你决定使用波士顿房价数据集，并且你的scikit-learn版本还包含这个数据集，你可以按照以下方式导入它：

from sklearn.datasets import load_boston
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target

上述代码加载了波士顿房价数据集，并将其分为特征数据X和目标数据y，以便后续进行机器学习模型的训练和评估。load_boston函数用于加载波士顿房价数据集，并将返回的数据集对象赋值给变量boston。boston.data提取特征数据，并将其赋值给变量X。boston.target提取目标数据（即房价），并将其赋值给变量y。

如果你使用的是较新的scikit-learn版本，或者你想要从一个CSV文件加载数据，你需要使用pandas库来读取数据。假设你有一个名为boston_housing.csv的CSV文件，它包含了与波士顿房价数据集相同的结构，你可以这样做：

import pandas as pd
from sklearn.model_selection import train_test_split
# 读取CSV文件
df = pd.read_csv('boston_housing.csv')
# 假设CSV文件的最后一列是目标变量（房价中位数），其余列是特征
X = df.iloc[:, :-1].values
y = df.iloc[:, -1].values

分割数据集

分割数据集主要是将数据集划分为训练集和测试集。训练集于训练决策树回归模型。在训练过程中，模型会学习特征变量（如波士顿房价数据集中的房间数、犯罪率等）和目标变量（房价）之间的关系。训练集是模型学习的主要数据来源。测试集用于评估模型的性能，在训练完成后，模型会使用测试集来进行预测，并通过比较预测值和实际值来评估模型的准确性。测试集帮助我们判断模型在未见过的数据上的泛化能力。

在实际应用中，我们通常需要对模型参数进行调整以获得更好的性能。通过分割数据集，我们可以使用训练集来训练不同参数配置的模型，并使用测试集来选择最佳参数配置。这样，我们可以确保所选参数在未见过的数据上仍然有效。

下面的Python代码将数据集分割为训练集和测试集：

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

该代码使用scikit-learn库中的train_test_split函数来将数据集分割成训练集和测试集，该函数接受特征矩阵X和目标向量y作为输入，并返回四个数组：训练集的特征（X_train）、测试集的特征（X_test）、训练集的目标值（y_train）和测试集的目标值（y_test）。

test_size=0.2：这个参数指定了测试集应该占整个数据集的比例。0.2意味着20%的数据将被用作测试集，而剩下的80%将被用作训练集。

random_state=42：这个参数是一个随机数生成器的种子。设置这个参数可以确保每次运行代码时，数据都以相同的方式被分割成训练集和测试集。这对于可重复的实验和结果验证是非常重要的。

四、创建决策树回归模型

预测房价最简单的模型就是根据以往的房价数据计算出均值，在不知道这些房子的任何信息的情况下，直觉上用平均值来预测是比较准确的。下面给出证明：

如果我们知道了房子的‌RM（每栋住宅的平均房间数），假设‌RM的值是1~10，如何能让这个信息帮助我们更加准确的预测房价呢？

一个思路是根据RM把房价分为两组，这两组分别应用之前提到的“平均值”模型。例如RM小于4的间住宅分到A组，大于或等于4间的住宅分到 B 组，A 组的评价房价是 10万美元，B 组的平均房价是18万美元。如果一套住宅的RM是3，应该被分到 A 组，模型就预测该套住宅的房价是10万美元。

我们可以绘制一个简单的决策树来表示根据RM（每栋住宅的平均房间数）预测房价的模型。这个决策树将RM值分为两组，并分别应用平均值模型来预测房价。以下是该决策树生成过程和图示：

决策树生成过程：

‌根节点‌：判断RM的值。

如果RM < 4，则进入‌左子节点‌（A组）。

如果RM >= 4，则进入‌右子节点‌（B组）。

‌左子节点‌（A组）：

预测房价为10万美元。

‌右子节点‌（B组）：

预测房价为18万美元。

决策树图示：

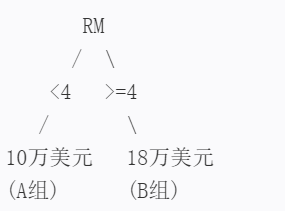
前面选择的房间数4不一定是最佳分割点，如何取一个最佳的分割点对不同房间数的住宅进行分组呢？

我们可以尝试所有可能的分割点。分割点就是一个房间数的值，我们根据这个值把房子分成两组：一组房间数小于这个值，另一组房间数大于或等于这个值。

对于每一个可能的分割点需要做以下几步：

‌分组‌：根据分割点把房子分成A组和B组。

‌计算损失‌：对A组和B组分别计算一个“损失值”（Loss），这个损失值反映了我们预测的平均价格与实际价格之间的差异。简单来说，就是看看我们预测得准不准，差异越小，损失值就越小。

‌求和‌：把A组和B组的损失值加起来，得到一个总的损失值（L_i）。

然后比较所有分割点得到的总损失值，找到最小的那个。最小的总损失值对应的分割点，就是我们要找的最佳分割点。

再复杂一些，如果我们不仅仅知道了住宅的RM（每栋住宅的平均房间数），还知道了住宅的‌AGE（房龄），该如何预测住宅的房价呢？

现在，我们不仅有房子的房间数（RM）信息，还有房子的房龄（AGE）信息。我们的目标是利用这两个信息来更准确地预测房子的价格。

‌找房间数的最佳分割点‌：

尝试所有可能的房间数值作为分割点，把房子分成两组：一组房间数小于这个值，另一组房间数大于或等于这个值。然后计算这两组的平均房价与实际房价之间的差异（也就是损失值L_1），找到使这个差异最小的分割点P_1。

‌找房龄的最佳分割点‌：

同样地也尝试所有可能的房龄值作为分割点，把房子分成两组，并计算损失值L_2。找到使这个损失值最小的分割点P_2。

现在有了两个分割点：一个是基于房间数的P_1，另一个是基于房龄的P_2。我们要比较这两个分割点对应的损失值L_1和L_2，看看哪个更小。

假设L_1比L_2小，这意味着按照房间数分组预测房价更准确。那么就选择P_1作为第一个分割点，把房子分成A组和B组（A组房间数小于P_1，B组房间数大于或等于P_1）。

接下来，在A组和B组内部，我们再分别考虑房龄信息：

‌在A组内找房龄的分割点‌：

对于A组内的房子，再尝试所有可能的房龄值作为分割点，把A组分成C组和D组（C组房龄小于某个值，D组房龄大于或等于这个值），并计算这两组的平均房价与实际房价之间的差异。找到使这个差异最小的分割点，这样A组就被分成了AC和AD两组。

‌在B组内找房龄的分割点‌：

同样地，对于B组内的房子，我们也找出使房价预测最准确的房龄分割点，把B组分成BC和BD两组。

现在，我们有了四组房子：AC、AD、BC和BD，每组都有一个对应的平均房价。当想要预测一个新房子的价格时，首先看它的房间数，决定它属于A组还是B组；然后，在这个组内再看它的房龄，决定它属于C组还是D组。最后用这组房子的平均房价作为预测价格。

决策树回归模型图示如下：

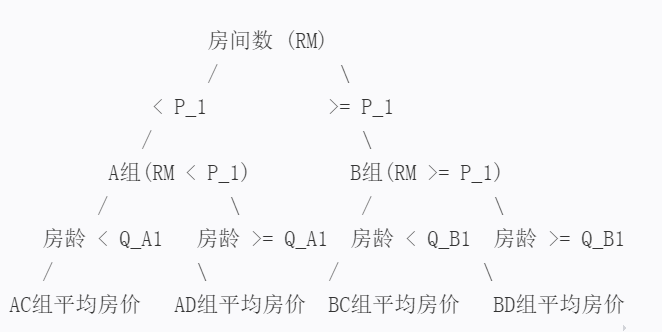
使用scikit-learn创建决策树回归模型，编写一条Python语句就可以了。

# 创建决策树回归模型实例
regressor = DecisionTreeRegressor(random_state=42)

该语句使用Python的scikit-learn库中的DecisionTreeRegressor类来创建一个决策树回归模型。

参数random_state用于控制决策树构建过程中的随机性。决策树在构建时可能会涉及一些随机过程，比如选择最佳分割点时如果有多个候选点具有相同的评估指标值，则可能会随机选择一个。通过设置random_state参数，我们可以确保每次运行代码时都会得到相同的结果，这对于实验的可重复性和调试是非常重要的。

五、训练模型

训练模型是将数据集输入到模型中，让模型通过学习算法来找到数据中的规律或模式。对于决策树回归模型来说，训练过程包括选择最优属性进行分裂、递归地构建树结构，直到满足停止条件（如达到最大深度、节点包含的样本数少于某个阈值等）。在这个过程中，模型会不断调整其参数或结构，以最小化损失函数（如均方误差），从而提高预测准确性。

‌使用scikit-learn训练模型，编写一条Python语句就可以了。

# 训练模型

regressor.fit(X_train, y_train)

regressor‌是一个已经实例化的决策树回归模型对象，fit()‌是模型对象的一个方法，用于训练模型。当调用这个方法时，模型会开始学习你提供的数据中的规律和模式。fit()方法通常需要两个参数：特征数据（X）和目标数据（y）。

当执行regressor.fit(X_train, y_train)时，实际上是在告诉regressor模型：“请使用X_train中的特征数据和y_train中的目标数据来训练你自己，以便你能够学习到如何根据特征来预测目标。”

在训练过程中，模型会：

（1）分析特征数据和目标数据之间的关系。

（2）调整模型内部的参数（对于决策树来说，可能是树的深度、分裂标准等）。

（3）尝试最小化预测误差，以便更好地拟合训练数据。

训练完成后，模型就可以用于对新的、未见过的数据进行预测了。

六、进行预测

一旦模型训练完成，它就可以用来对新的、未见过的数据进行预测。本案例中预测用的数据为X_test，预测结果与y_test进行比对，已评估模型的性能。

下面的python语句完成模型预测：

# 进行预测

y_pred = regressor.predict(X_test)

predict()‌是模型对象的一个方法，用于对新的输入数据（在这个例子中是 X_test）进行预测。

七、评估模型

比较 y_pred 和测试数据的真实目标值 y_test，计算性能指标（如均方误差、R² 分数等）来评估模型的预测能力。通过评估，可以了解模型在未知数据上的表现，从而判断其泛化能力‌。

# 计算均方误差（MSE）
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

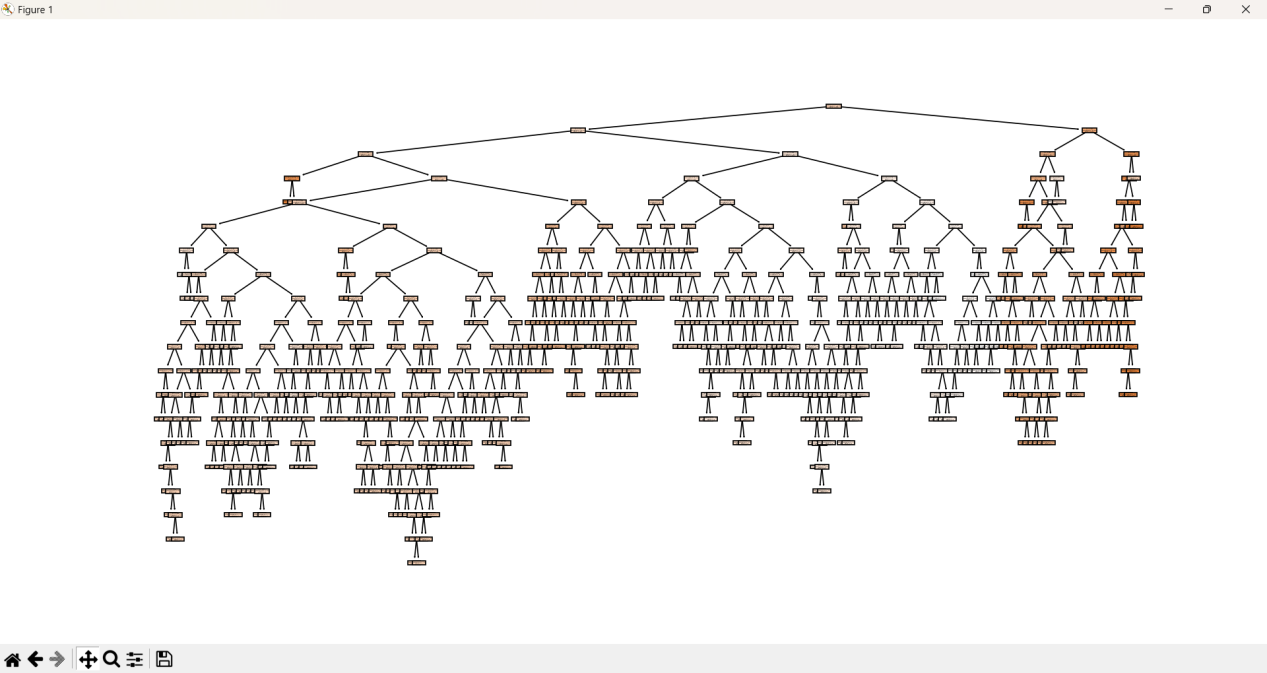
八、可视化

为了更好地理解模型，可以使用matplotlib或scikit-learn的plot_tree函数来可视化决策树。

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
plt.figure(figsize=(20,10))
plot_tree(regressor, filled=True, feature_names=X.columns, class_names=True)
plt.show()

决策树图示：