计算机基础：计算机与二进制

今天的课程是数据在计算机中的表示，重点讲述二进制计数、数制的转换，最后简单归纳一下数据在计算机中的存储方式。

0和1的组合

0和1的组合是一个非常神奇的组合，因为用0和1可以描述灯泡的亮与不亮、电路的通与断。

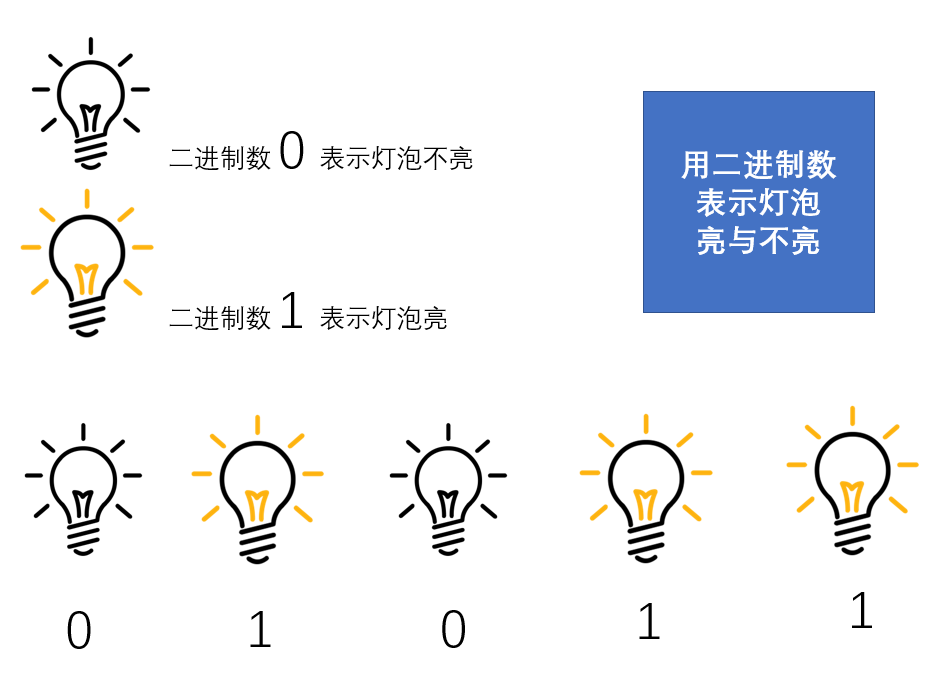
可以使用0和1来表示多个灯泡的亮与不亮，用0表示灯泡不亮，用1表示灯泡亮，图中0和1的组合01011完整描述了5个灯泡的当前状态。
0和1也可以描述电路电位的高低，高位为，低位为0。计算机的电路都是由电子元器件构成的，通电的电子元器件两端会有电压，称为高电位，用1来表示，没有通电的电子元器件两端没有电压，称为低电位，因此一组由电子元器件构成的电路可以使用0和1的组合来表示。

上图0101描述了四只二极管的组合状态，显然左数第2和第4只二极管处于高电位，第1和第3只二级管处于低电位。实际上，可以使用四只二级管表示16个状态，如设备的多个状态，也可以表示1至16的数字，如0001表示数字1,0002表示数字2，……；也可以表示16个字符，如0001表示字符A，0002表示字符B，……。
计算机是由电子元器件构成的，因此0和1是计算机可识别的唯一语言，0和1的组合也称为二进制数，计算机除使用二进制数表示数据外，还可以进行数值和逻辑运算。

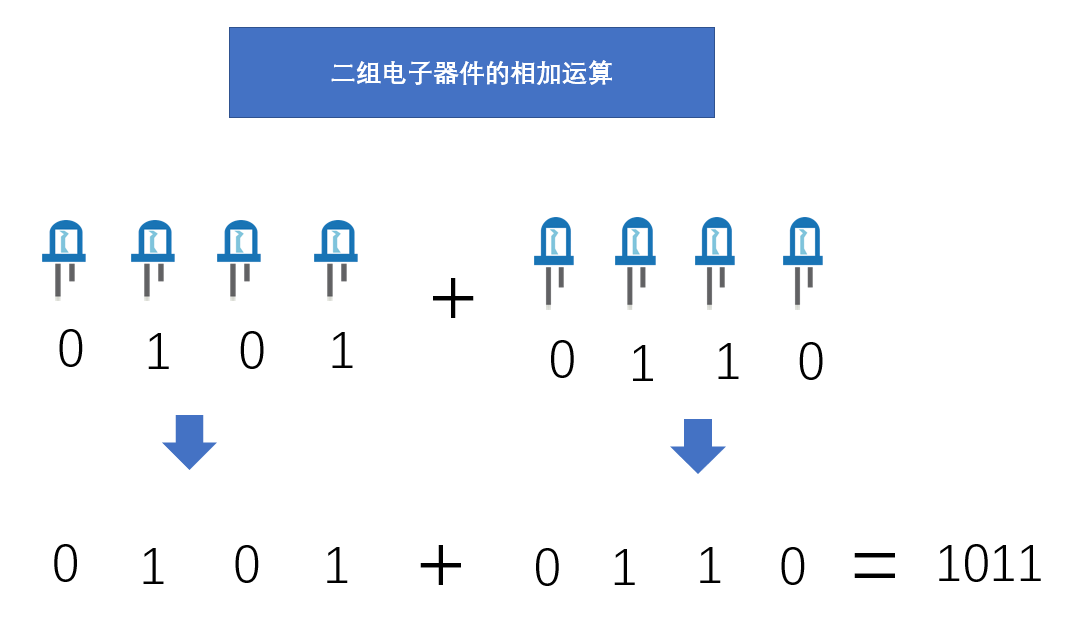
电子元器件状态的二进制可以进行最简单的加减运算（再复杂的运算最终都会分解为加减运算），运算后的结果再通过控制电路改变电子元器件的状态。因此计算机内部运算都采用二进制运算，能够识别的数也是二进制数。

认识二进制数

我们通过一个小游戏来认识二进制数。
伸出我们的右手，从小指开始，依次到大拇指分别代表数字1、2、4、8、16，这些数字也称为每个手指的权重，拇指的权重是16，食指的权重为8，中指的权重为4，无名指的权重为2，小指的权重为1。并且每个手指分为两种状态，手指伸直为1状态，手指弯曲为0状态。如下图所示。

分别做每个手指自由伸直或弯曲动作，记录其状态和五个手指的数字之和，状态顺序从大拇指开始。记录五个手指的状态与权重乘积的和。

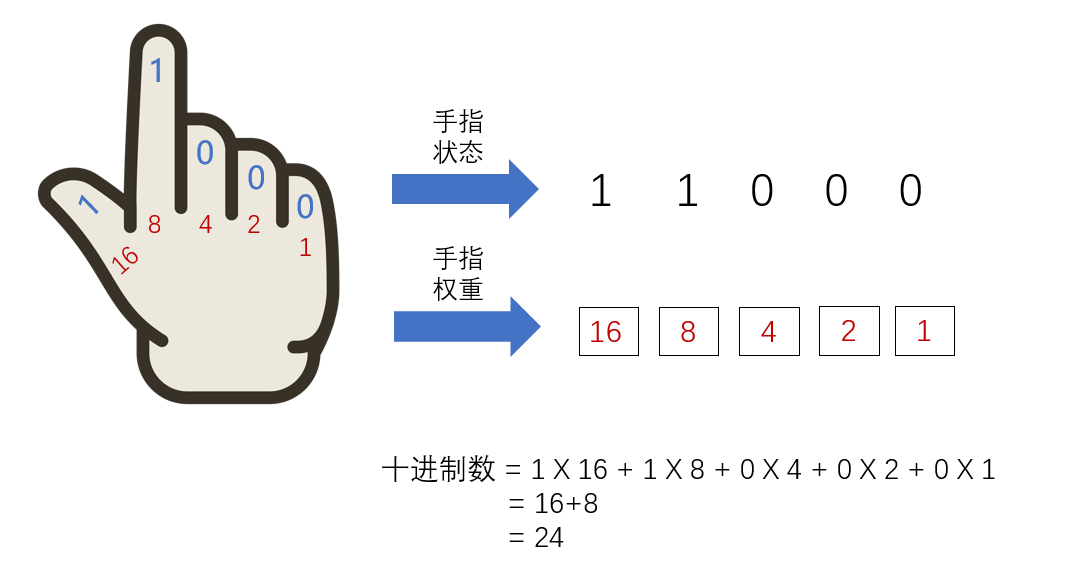
动作1
动作：伸直小指、中指和大拇指，弯曲无名指和食指。
状态：10101
数字之和：1X16+0X8+1X4+0X2+1X1=21
动作2
动作：伸直小指、无名指和中指，弯曲大拇指和食指。
状态：00111
数字之和：0X16+0X8+1X4+1X2+1X1=7

游戏用直观化的方式演示了二进制数到十进制数的转换，五个手指的伸直和弯曲的状态组合用0和1表述出来。数字之和就是二进制数的十进制表示。

可以借助十进制数来理解二进制数。在十进制中，最开始学习的是十以内的加法，之后是两位数的加法，在两位数加法的学习中，就需要逢十进一了，按进位的原则进行记数的方法叫做进位记数制，也称为“数制”或“进制”。

生活中人们常用的数制为十进制和六十进制，计算机中常用的数制为二进制、十进制、十六进制。每一种数制的进位都遵循一个规则，那就是——逢n进1。这里的n叫做基数。例如：十进制逢10进1，二进制逢2进1，十六进制逢16进1，六十进制逢60进1，时间就是六十进制。

一个数制的基数也表示该数制由多少个数字构成，例如：十进制的基数是10，它由10个数字构成；二进制的基数是2，它由2个数字构成；十六进制的基数是16，它由16个数字构成。
在十进制计数中，计数单位分别为个位、十位、百位、千位、万位、十万位……，其中个位数表示数值1、十位数表示数值10、百位数表示数值100、千位数表示数值1000、……，每个位数表示的数值叫位权。

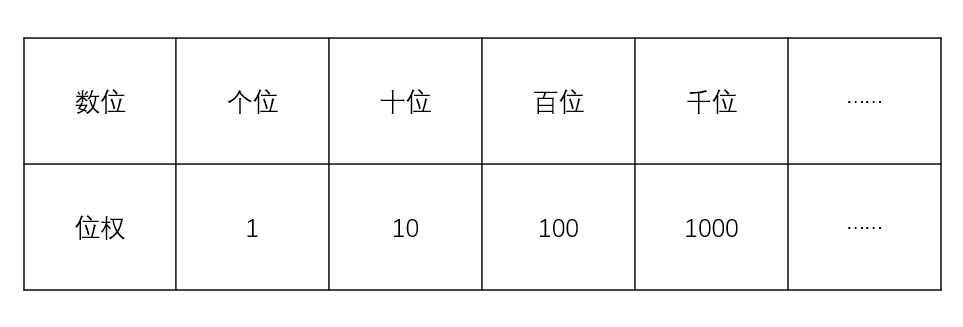
例如十进制数1260，千位1位权是10^3，百位2位权是10^2，十位6位权是1，个位0位权是0。

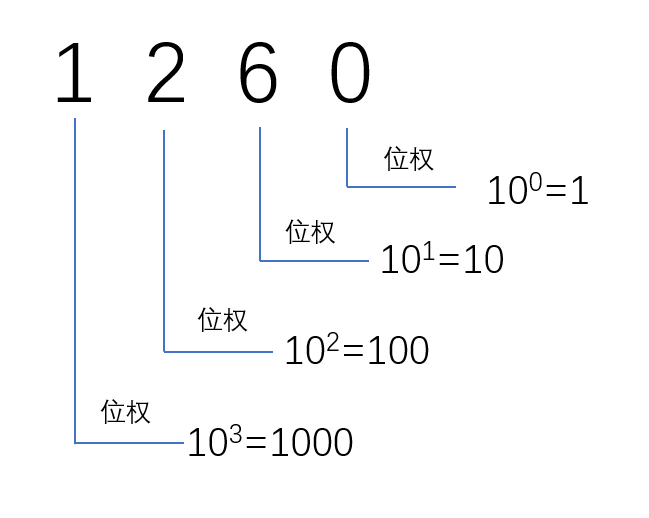
应用位权，1260也可以分解成下面的算式：
1260 = 1 X 10^3 + 2 X 10^2 + 6 X 10^1 + 0 X 10^0
理解了十进制的位权，再来理解二进制的位权就很容易了。例如，二进制数1100从低位到高位的位权依次是2^0，值是1、2^1，值是2、2^2，值是4、2^3次，值是8，这也是前面从小指开始到食指指定的位权。

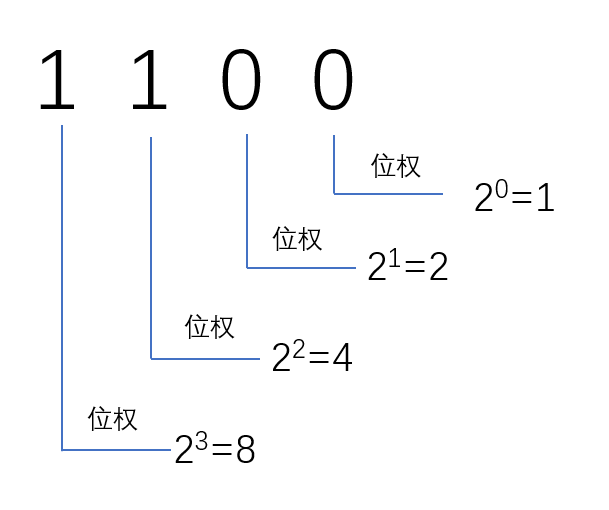
数制转换

了解了不同数制的位权，进行数制转换就非常简单了。把二进制数转换为十进制数应用“按权相加法”，即把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。
例如：把二进制数1011.11转换成十进制数。

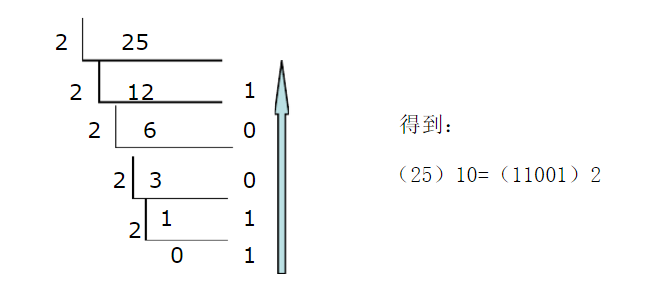
十进制转换为二进制采用“除2取余，逆排序法”。具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为零时为止，然后把所有余数按逆序排列，也就是把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
例如：将一个十进制数25转换为二进制数。

虽然计算机采用二进制表示数据，但书写二进制数比较麻烦，因此人们经常使用十六进制来表示二进制数，十六进制的基数是16，数码为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F，其中用A，B，C，D，E，F（字母不区分大小写）这六个字母来分别表示10，11，12，13，14，15。

十六进制转换为二进制数，还是应用“按权相加法”。例如：

为了区分不同的数制，在计算机编程语言中，通常用数字后面跟一个英文字母来表示该数的数制。
十进制一般用D（Decimal）
二进制数用B（Binary）
十六进制用H（Hexadecimal）
例如：23AH、570D、110101B、0075H，…。当然也可以用这些字母的小写形式。

十六进制转换为二进制非常容易，由于十六进制的基数是2的幂，所以这两种数制之间的转换是十分容易的。一个二进制数，只要把它从低位到高位每4位组成一组，直接用十六进制数来表示就可了。

最后，我们在聊聊在计算机科学中，是如何使用二进制来表示数据的。

数值、文本、音视频和图片是人们经常使用的数据。
数值数据中，人们擅长使用的是十进制数，当人们使用键盘输入数字时，需要输入程序把数字转换为二进制数输入到计算机，计算机显示数字时，需要输出程序把二进制数转换为十进制数。
文本数据中，人们输入各种字符时，需要输入程序将字符进行编码，编码用二进制数表示，计算机显示字符时，需要输出程序匹配与编码对应的字符信息，字符信息一般存储在一个称为字库的文件，该文件存储了字符的图形数据，计算机显示字符的图形数据。
音视频和图片数据在计算机中二进制编码方式存储，在输出音视频和图片数据时使用特定程序进行解码输出。