应用Scipy完成插值运算
- SciPy数值计算
- 2024-11-08
- 659热度
- 0评论
什么是插值
插值是一种利用已知数据点来估算未知数据点数值的方法,它通过一定的算法或公式,填充或预测缺失的数据。简单来说插值是一种在给定的点之间生成新点的方法。
我们通过一个简单的案例来理解插值运算。
假设我们有两个已知的数据点:(1, y1) 和 (2, y2),其中y1和y2是这两个点对应的函数值(在实际应用中,这些值可能是通过实验、测量或计算得到的)。现在需要在x=1.5这个位置找到一个插值点,即估算出当x=1.5时,y的值是多少。
具体计算步骤为:
- 确定已知点:已知点(1, y1)和(2, y2)。
- 计算插值点的x坐标与已知点x坐标的差:插值点的x坐标为5,所以与1的差是0.5,与2的差是-0.5。
- 应用线性插值公式: Y = ( ( X - X1 )( Y2 - Y1) / ( X2 - X1) ) + Y1
其中x1, y1, x2, y2是已知点的坐标,x是插值点的x坐标,y是我们要找的插值点的y坐标。代入数值计算,得y = 1.5。所以,当x=1.5时,通过线性插值估算出的y值为1.5。
这个简单例子展示了如何在两个已知点之间进行线性插值。在实际应用中,插值方法可能会更加复杂,但基本原理都是利用已知数据点来估算未知数据点的值。
线性插值
线性插值是指插值函数为一次多项式的插值方式,,简单来说,就是一种利用两个已知点之间的直线关系,来估算出这两个点之间任意一个新点的y值的方法。这种方法在很多领域都很有用,比如数据分析、图像处理、工程计算等。
线性插值分为单线性插值和多线性查找。单线性插值是根据一维数据序列中需要插值的点的左右邻近两个数据点,通过直线方程来估计未知数值的方法。多线性插值是指在多维空间中,利用已知数据点构建一个多维线性函数,来估算其他未知点值的方法,它基于线性插值原理,将一维线性插值扩展到多维情况。对于二维数据,双线性插值是最常见的形式,通过相邻的四个数据点构建一个平面来估算中间点的值。
scipy.interpolate模块提供了计算线性插值的方法。
单线性插值案例
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import matplotlib
# 配置Matplotlib以支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体,或者其他支持中文的字体
matplotlib.rcParams['axes.unicode_minus'] = False # 正确显示负号
# 原始数据点
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 3, 5, 7, 11])
# 创建线性插值器
linear_interp = interp1d(x, y)
# 插值点
x_interp = np.array([1.5, 2.5, 3.5, 4.5]) # 选择一些位于原始数据点之间的点进行插值
y_interp = linear_interp(x_interp) # 计算插值点的y值
# 可视化
plt.figure(figsize=(8, 6))
# 绘制原始数据点
plt.plot(x, y, 'o', label='原始数据点', markersize=8)
# 绘制插值点
plt.plot(x_interp, y_interp, 'rx', label='插值点', markersize=10) # 使用红色叉号表示插值点
# 使用线性插值器绘制整个插值曲线(可选,主要用于展示插值效果)
x_full = np.linspace(x.min(), x.max(), 100)
y_full = linear_interp(x_full)
plt.plot(x_full, y_full, '--', label='线性插值曲线', linewidth=2)
# 添加图例和标签
plt.legend()
plt.xlabel('x 值')
plt.ylabel('y 值')
plt.title('单线性插值示例')
# 显示图形
plt.grid(True)
plt.show()
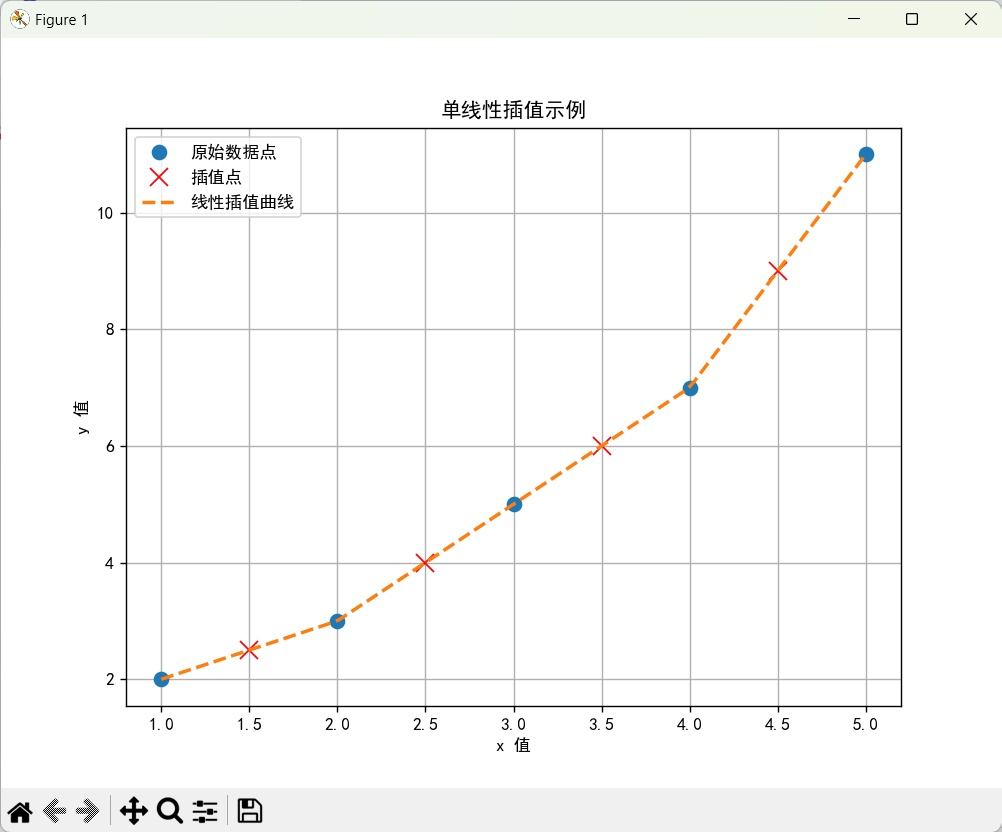
示例代码首先定义了原始数据点x和y,然后使用interp1d函数创建了一个线性插值器linear_interp。接着选择一些位于原始数据点之间的点x_interp进行插值,并计算了这些点的y值(即y_interp)。最后使用matplotlib.pyplot绘制了原始数据点、插值点以及整个插值曲线,以便直观地展示插值效果。
代码运行后,示例结果如下图。
多线性插值案例
import numpy as np
from scipy.interpolate import griddata
import matplotlib.pyplot as plt
import matplotlib
# 配置Matplotlib以支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体,或者其他支持中文的字体
matplotlib.rcParams['axes.unicode_minus'] = False # 正确显示负号
# 原始数据点(不规则)
x = np.random.rand(10) * 10 # x 坐标,范围在 0 到 10 之间
y = np.random.rand(10) * 10 # y 坐标,范围在 0 到 10 之间
z = np.sin(x/10) * np.cos(y/10) # 假设这是某个函数在这些点上的值
# 插值点(规则网格)
xi = np.linspace(0, 10, 100)
yi = np.linspace(0, 10, 100)
xi, yi = np.meshgrid(xi, yi)
# 多线性插值
zi = griddata((x, y), z, (xi, yi), method='linear')
# 可视化
plt.figure(figsize=(8, 6))
# 绘制原始数据点
plt.scatter(x, y, c=z, marker='o', label='原始数据点', cmap='viridis')
# 选择一些插值点进行标记(这里选择网格的中心点作为示例)
center_idx = len(xi) // 2
center_x = xi[center_idx, center_idx]
center_y = yi[center_idx, center_idx]
center_z = zi[center_idx, center_idx]
plt.scatter(center_x, center_y, c=center_z, marker='x', s=100, label='标记的插值点', cmap='viridis')
# 绘制插值结果的等高线图
plt.contourf(xi, yi, zi, levels=50, cmap='viridis', alpha=0.7)
plt.colorbar()
# 添加图例和标签
plt.legend()
plt.xlabel('x 值')
plt.ylabel('y 值')
plt.title('多线性插值示例(二维)')
# 显示图形
plt.grid(True)
plt.show()
代码执行后,输出结果见下图。
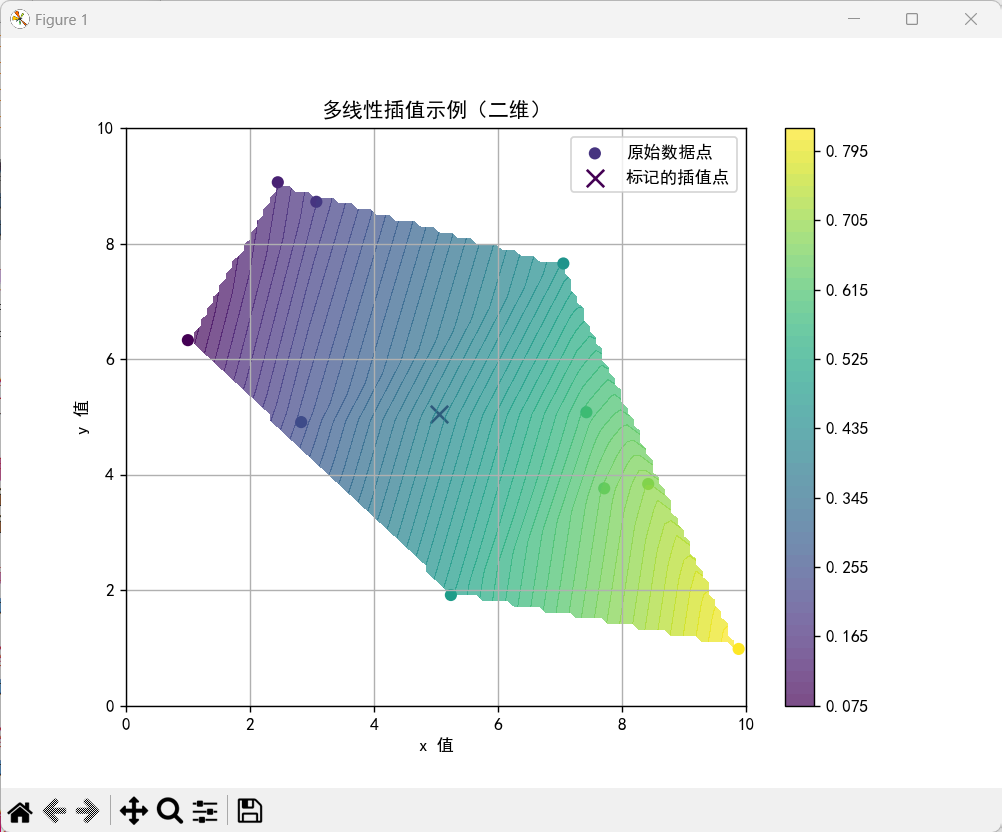
示例代码首先生成了一些不规则的原始数据点,并计算了这些点上某个函数的值。然后创建了一个规则的网格,并使用griddata函数在这个网格上进行了多线性插值。代码绘制了原始数据点、插值结果的等高线图(等高线图是一种展示二维插值结果的直观方式),并选择网格的中心点作为示例来标记一个插值点。
当前示例只标记了一个插值点,在实际应用中,可能需要选择标记更多的插值点。
多项式插值
多项式插值是用一个多项式去近似任意的函数。简单来说,就是找到一个插值多项式,使其恰好通过这些数据点,然后通过这个插值多项式来评估在任意点上的函数值,一般是将点的横坐标代入插值多项式并计算得到的结果来实现的。
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import BarycentricInterpolator
import matplotlib
# 配置Matplotlib以支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
# 原始数据点
x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 4, 9, 16, 25])
# 使用numpy.polyfit拟合多项式(这里选择二次多项式)
degree = 2
coefficients = np.polyfit(x, y, degree)
# 使用numpy.polyval评估多项式在指定点上的值(这里选择原始数据点之间的点进行插值)
x_interp = np.linspace(x.min(), x.max(), 100)
y_interp = np.polyval(coefficients, x_interp)
# 可视化
plt.figure(figsize=(8, 6))
# 绘制原始数据点
plt.plot(x, y, 'o', label='原始数据点', markersize=8)
# 绘制插值曲线
plt.plot(x_interp, y_interp, '-', label='二次多项式插值曲线', linewidth=2)
# 如果需要,也可以使用scipy的BarycentricInterpolator进行Lagrange插值
# interpolator = BarycentricInterpolator(x, y)
# y_interp_scipy = interpolator(x_interp)
# plt.plot(x_interp, y_interp_scipy, '--', label='Lagrange插值曲线', linewidth=2)
# 添加图例和标签
plt.legend()
plt.xlabel('x 值')
plt.ylabel('y 值')
plt.title('多项式插值示例')
# 显示图形
plt.grid(True)
plt.show()
代码执行后,输出结果见下图。
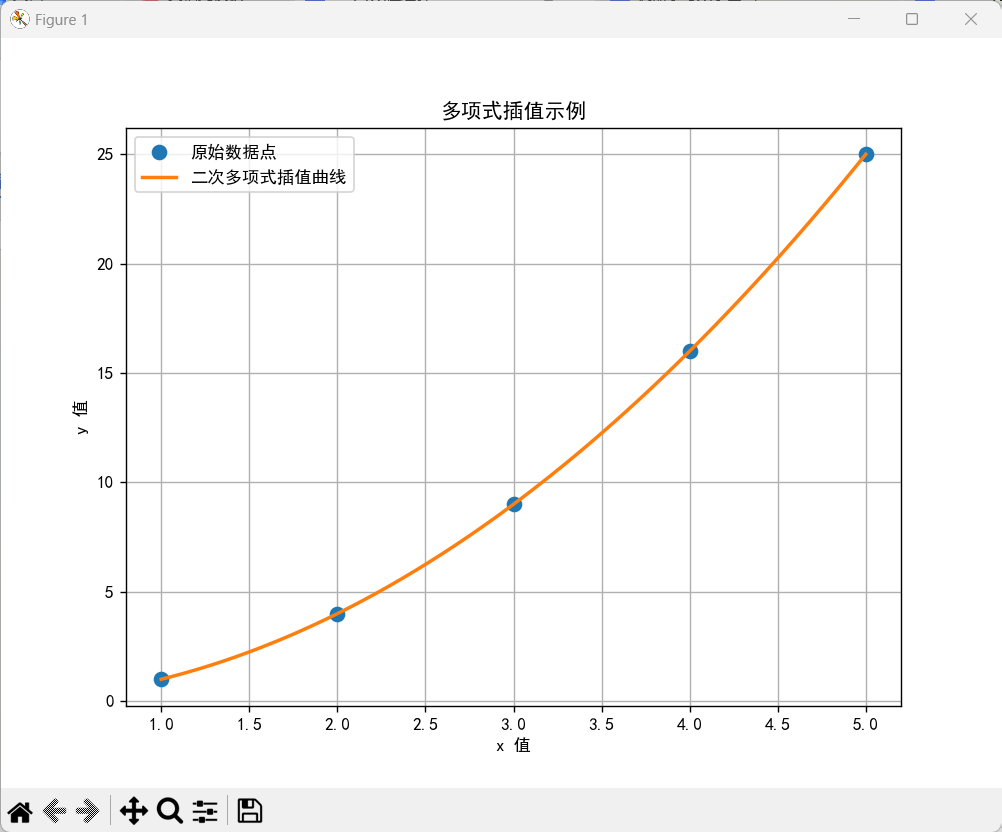
示例代码首先使用numpy.polyfit函数根据原始数据点拟合了一个二次多项式,得到了多项式的系数。然后使用numpy.polyval函数评估了这个多项式在指定点(这里是一个介于原始数据点之间的线性空间)上的值,得到了插值结果。最后使用matplotlib.pyplot绘制了原始数据点和插值曲线。
分段插值
分段插值就是把一组数据点分成好几段,然后每一段都单独用一个简单的函数(如线性函数、多项式等)来近似表示这些数据点之间的变化规律。
分段插值把一组数据分成小段,然后用简单的函数来拟合每段数据的变化。对于每一段来说,函数都比较简单,容易计算和理解。同时,因为每段都是单独处理的,所以即使有些段的变化比较复杂,也不会影响到其他段。
假设我们有一组三维空间中的已知点,我们希望在这些点之间进行插值。具体计算步骤:
- 对已知点进行排序,以确保插值是在有序的数据点上进行;
- 应用三次样条插值法求已知数据点的拟合函数;
- 使用拟合函数计算新增加点的数据。
Python代码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.interpolate import make_interp_spline
import matplotlib
# 配置Matplotlib以支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
# 已知的三维空间点
points = np.array([[2.1, 4, 1], [3.2, 4.1, 1.5], [5.5, 3.8, 1.2], [7.0, 4.5, 2.0]])
x = points[:, 0]
y = points[:, 1]
z = points[:, 2]
# 对x进行排序,以确保插值是在有序的数据点上进行
sorted_indices = np.argsort(x)
x_sorted = x[sorted_indices]
y_sorted = y[sorted_indices]
z_sorted = z[sorted_indices]
# 创建分段插值函数
spl_x = make_interp_spline(x_sorted, y_sorted, k=3) # k=3表示三次样条插值
spl_z = make_interp_spline(x_sorted, z_sorted, k=3) # 对z也进行三次样条插值
# 生成新的x值用于插值
x_new = np.linspace(x_sorted.min(), x_sorted.max(), 100)
# 使用插值函数计算新的y值和z值
y_new = spl_x(x_new)
z_new = spl_z(x_new)
# 可视化原始点和插值点
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, color='blue', label='原始数据点')
ax.scatter(x_new, y_new, z_new, color='red', label='插值点')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.legend()
plt.show()
代码执行后,输出结果见下图。
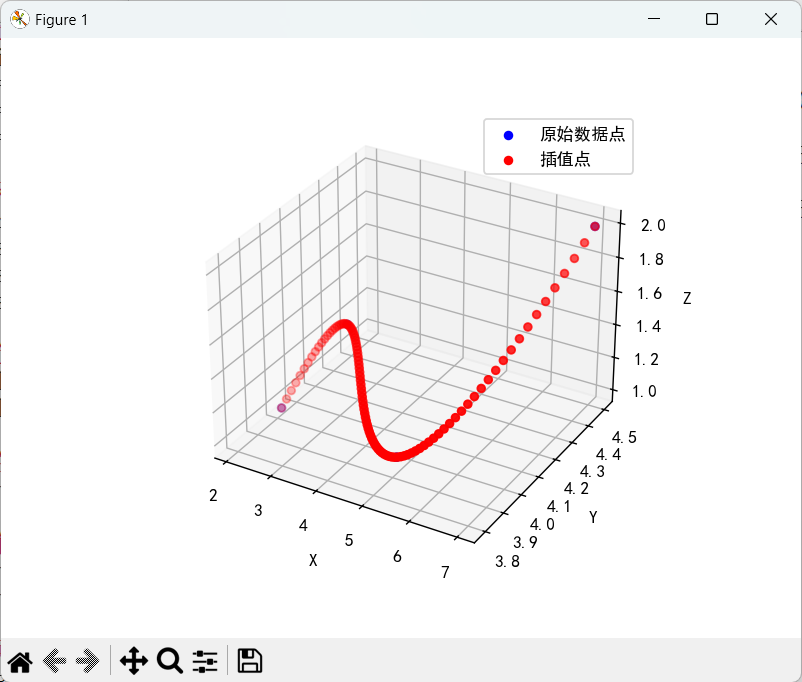
示例代码片段使用NumPy、Matplotlib和SciPy库进行三维空间点的插值和可视化。首先使用NumPy数组定义四个三维空间点,并对x坐标进行排序,以确保插值是在有序的数据点上进行。然后使用make_interp_spline创建两个三次样条插值函数,一个用于y坐标,一个用于z坐标,均以x坐标为自变量。再生成新的x值,使用插值函数计算新的y值和z值。最后使用Matplotlib显示原始数据点和插值点,并使用不同颜色区分。