对鸢尾属植物数据集进行统计分析与可视化

关于鸢尾属植物集

鸢尾属植物数据集最初由统计学家与生物学家Ronald Fisher在1936年的论文《The use of multiple measurements in taxonomic problems》中提出。数据集中的样本由Edgar Anderson测量得到，而后被Fisher用于其论文中，作为线性判别分析（Linear Discriminant Analysis）的一个例子，用以证明分类的统计方法。

鸢尾属植物数据集包含了150个鸢尾属植物样本，每个样本有4个特征：萼片长度（sepal length）、萼片宽度（sepal width）、花瓣长度（petal length）和花瓣宽度（petal width）。这个数据集通常用于分类任务，目标是区分三种不同的鸢尾属植物：山鸢尾（Iris Setosa）、杂色鸢尾（Iris Versicolour）和维吉尼亚鸢尾（Iris Virginica）。

鸢尾花数据集在机器学习领域被广泛应用于模式识别、分类算法的验证和数据可视化等方面。

加载鸢尾属植物数据集

鸢尾属植物数据集可以通过Python的sklearn库在线下载，sklearn库是是机器学习领域常用的库，涉及数据预处理、特征提取、模型选择和评估等多个方面。本文借助sklearn库的datasets模块下载鸢尾属植物数据集到本地。

Python代码：

import pandas as pd
from sklearn.datasets import load_iris

# 加载鸢尾属植物数据集
iris_data = load_iris()

# 将数据集转换为Pandas DataFrame
iris_df = pd.DataFrame(data=iris_data.data, columns=iris_data.feature_names)

描述统计性分析

描述统计性分析通过均值、中位数、众数、方差、标准差、频数分布、直方图、箱线图等，来概括和描述数据集的特征。这些统计量和图形提供了数据的集中趋势、离散程度和分布形态等信息，使我们能够更直观地理解数据。
‌均值‌：反映数据的平均水平，但易受极端值影响。
‌中位数‌：将数据从小到大排序后，位于中间位置的数值，不受极端值影响。
‌众数‌：数据集中出现次数最多的数值，用于描述数据的集中点。
‌方差与标准差‌：衡量数据的离散程度，方差是各数据与其均值之差的平方的平均数，标准差是方差的平方根。
‌四分位数‌：将数据从小到大排序后，将数据分为四等份的数值，分别为下四分位数（Q1）、中位数（Q2）和上四分位数（Q3）。四分位距（IQR）是Q3与Q1之差，用于衡量数据分布的中间部分。
例1：计算花萼长度的均值、中位数、标准差和众数

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
import seaborn as sns
from sklearn.datasets import load_iris

# 配置Matplotlib以支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体，或者其他支持中文的字体
matplotlib.rcParams['axes.unicode_minus'] = False # 正确显示负号

# 加载鸢尾属植物数据集
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)

# 选择花萼长度列
sepal_length = df['sepal length (cm)']

# 计算统计量
mean_sepal_length = sepal_length.mean()
median_sepal_length = sepal_length.median()
std_sepal_length = sepal_length.std()
mode_sepal_length = sepal_length.mode()[0] # 众数，可能有多个，这里取第一个

# 输出统计量
print(f"花萼长度的均值: {mean_sepal_length:.2f} cm")
print(f"花萼长度的中位数: {median_sepal_length:.2f} cm")
print(f"花萼长度的标准差: {std_sepal_length:.2f} cm")
print(f"花萼长度的众数: {mode_sepal_length:.2f} cm")

# 可视化
plt.figure(figsize=(12, 6))

# 直方图
sns.histplot(sepal_length, kde=True, bins=30, color='skyblue', linewidth=0)
plt.axvline(mean_sepal_length, color='r', linestyle='dashed', linewidth=1, label=f'均值: {mean_sepal_length:.2f}')
plt.axvline(median_sepal_length, color='g', linestyle='dashed', linewidth=1, label=f'中位数: {median_sepal_length:.2f}')

# 添加标题和标签
plt.title('鸢尾属植物花萼长度的分布')
plt.xlabel('花萼长度 (cm)')
plt.ylabel('频数')
plt.legend()
plt.grid(True)

# 显示图形
plt.show()

绘制的统计图：

从统计图可以得出如下结论：
（1）所有样本花萼长度的中心趋势为5.84cm，即花萼长度的平均长度为5.84cm；
（2）有一半的样本花萼长度小于5.80cm，另一半大于5.80cm；
（3）‌标准差为0.83 cm的花萼长度说明该长度分布相对集中，大多数花萼长度都在平均值附近；
（4）数据集中出现次数最多的花萼长度值5.00cm。

相关性分析

对于萼片长度（sepal length）、萼片宽度（sepal width）、花瓣长度（petal length）和花瓣宽度（petal width）这四个变量，相关性分析可以帮助我们了解它们之间的关系强度和方向。
在进行相关性分析时，通常会计算每对变量之间的相关系数，如皮尔逊相关系数。这个相关系数会告诉我们两个变量之间是否存在线性关系，以及这种关系的强度和方向（正相关或负相关）。
例如，如果统计发现花瓣长度和花瓣宽度之间有一个高的正相关系数，那么这意味着当花瓣长度增加时，花瓣宽度也倾向于增加。相反，如果两个变量之间的相关系数接近零，那么它们之间可能没有线性关系。

例2：变量间相关性分析

import pandas as pd
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# 配置Matplotlib以支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体，或者其他支持中文的字体
matplotlib.rcParams['axes.unicode_minus'] = False # 正确显示负号

# 加载鸢尾属植物数据集
iris = load_iris()
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
# 计算相关性矩阵
corr_matrix = df.corr()

# 绘制相关性热力图
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt='.2f')

# 添加标题和标签
plt.title('鸢尾属植物数据集特征相关性热力图')
plt.xlabel('特征')
plt.ylabel('特征')

# 显示图形
plt.show()

# 分析相关性结果
print("相关性矩阵：")
print(corr_matrix)

绘制的统计图：

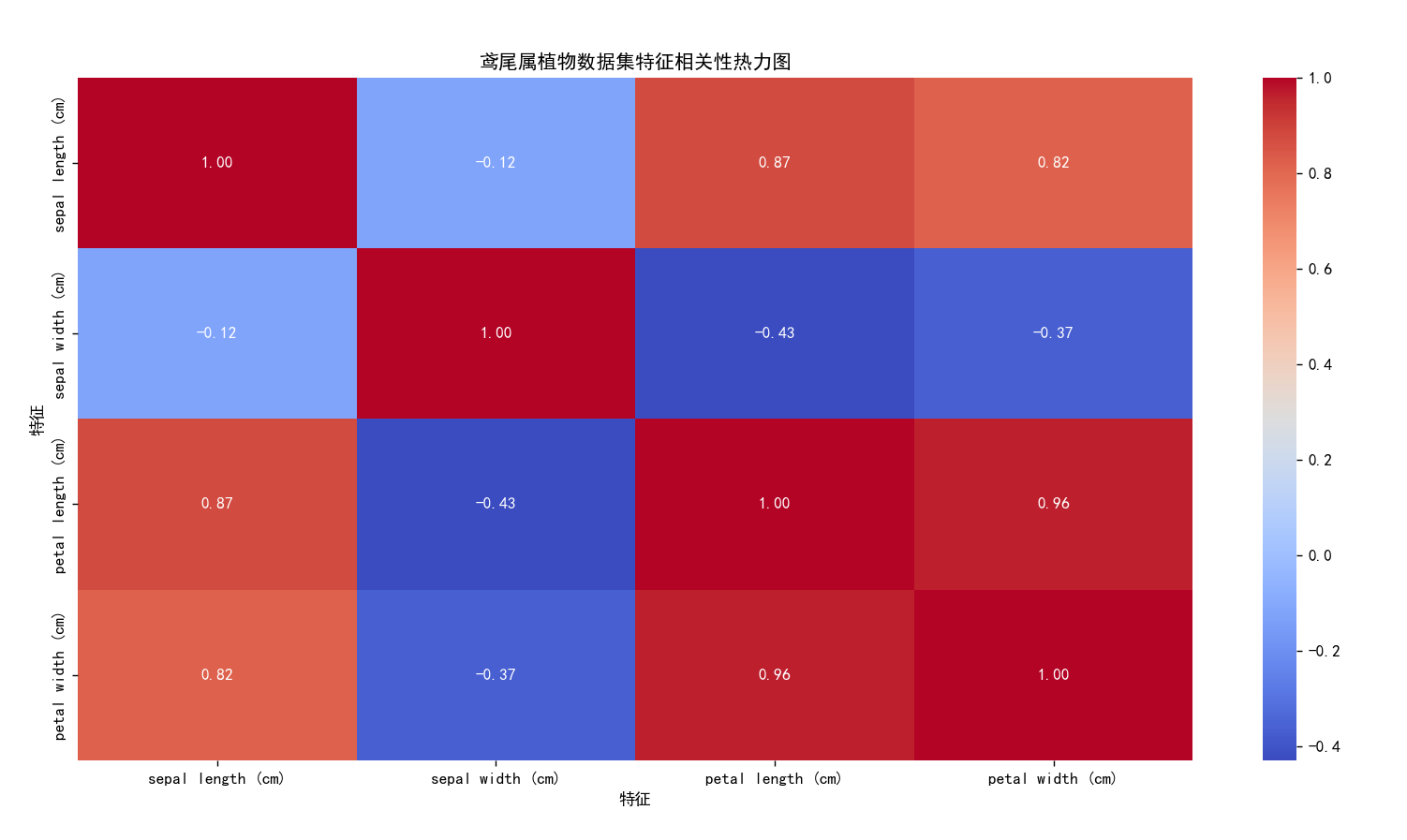
从统计图可以得出如下结论：
花萼长度与花萼宽度‌：通常有一定的正相关性，因为较长的花萼通常也较宽。
‌花瓣长度与花瓣宽度‌：也有一定的正相关性，较长的花瓣通常也较宽。
‌花萼长度与花瓣长度‌：相关性较低，因为这两种特征分别描述了花的两个不同部分。
‌花萼宽度与花瓣长度‌：相关性也较低，因为它们分别描述了花的两个不同部分。