SciPy信号处理：傅里叶变换

假设我们有一个包含噪声的音频信号，目标是使用傅里叶变换来识别信号中的频率成分，并据此来过滤掉噪声，最后通过傅里叶逆变换还原出纯净的信号。以下是信号处理步骤。

生成信号

生成一个正弦波信号作为原始信号。这个信号具有一定的频率和幅值，并且持续一段时间。再生成一个高频的噪声信号，并将其与原始信号混合，以模拟带有噪声的音频信号。

傅里叶变换

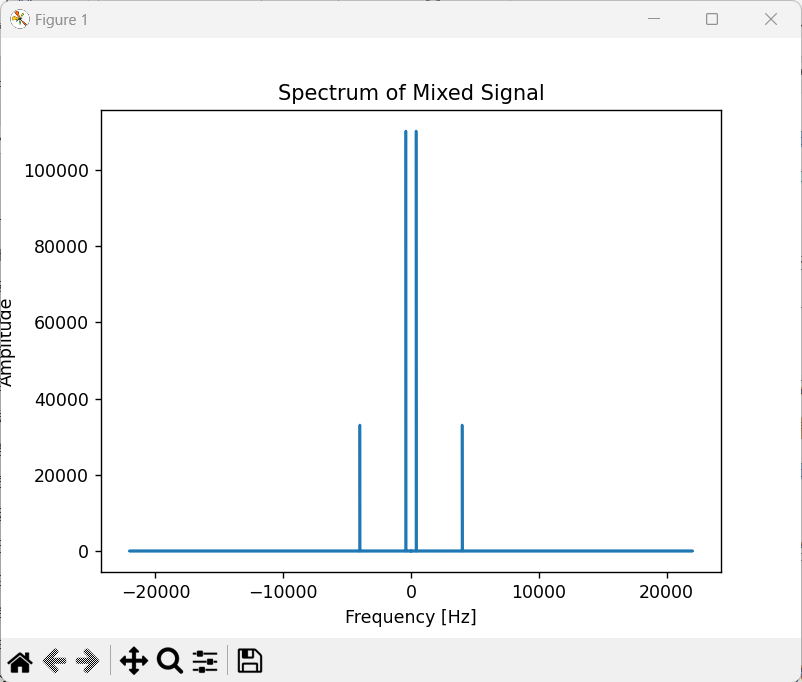
使用SciPy库中的fft函数对混合信号进行傅里叶变换。将时域信号转换为频域信号，使我们能够分析信号中的频率成分。绘制频谱图，观察混合信号的频率分布。在频谱图中，可以看到由原始信号和噪声信号组成的两个主要的频率峰值。

过滤噪声

根据频谱图，确定要移除的噪声信号的频率范围。在频域中，将对应噪声频率的信号置为零，以去除噪声。

傅里叶逆变换

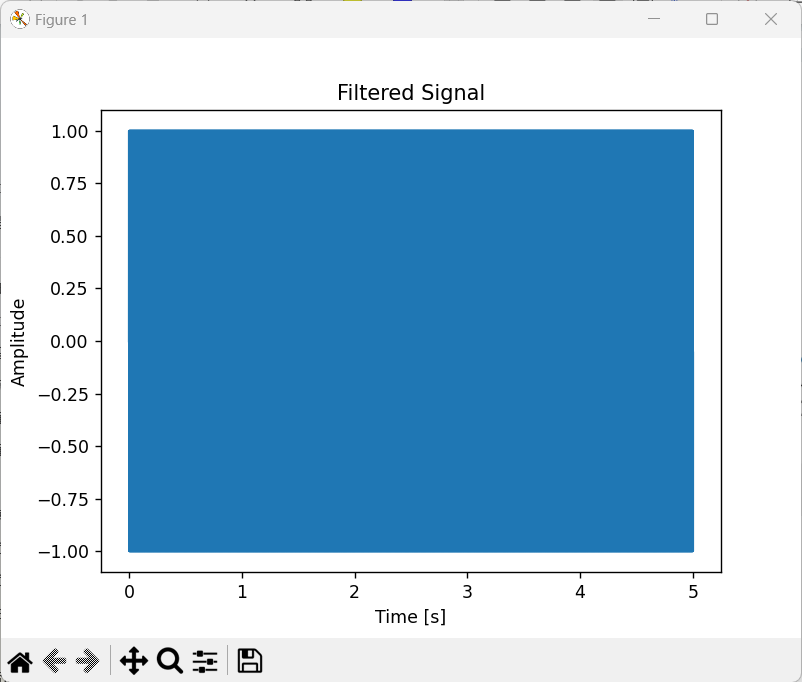
使用SciPy库中的ifft函数对处理后的频域信号进行傅里叶逆变换，将其转换回时域信号。绘制处理后的时域信号波形图，观察去除噪声后的效果。
案例代码：

import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq, ifft

# 生成信号参数
SAMPLE_RATE = 44100 # 采样率
DURATION = 5 # 信号持续时间（秒）
FREQ_SIGNAL = 400 # 原始信号频率（Hz）
FREQ_NOISE = 4000 # 噪声信号频率（Hz）

# 生成时间序列
t = np.linspace(0, DURATION, SAMPLE_RATE * DURATION, endpoint=False)

# 生成原始信号和噪声信号
signal = np.sin(2 * np.pi * FREQ_SIGNAL * t)
noise = 0.3 * np.sin(2 * np.pi * FREQ_NOISE * t) # 噪声信号的幅值为原始信号的0.3倍

# 混合信号
mixed_signal = signal + noise

# 傅里叶变换
N = SAMPLE_RATE * DURATION # 采样点数
yf = fft(mixed_signal) # 快速傅里叶变换
xf = fftfreq(N, 1 / SAMPLE_RATE) # 计算频率轴

# 绘制频谱图
plt.plot(xf, np.abs(yf))
plt.xlabel('Frequency [Hz]')
plt.ylabel('Amplitude')
plt.title('Spectrum of Mixed Signal')
plt.show()

# 过滤噪声
# 找到噪声频率对应的索引，并将其置为零
target_idx = np.squeeze(np.argwhere(np.abs(xf) == FREQ_NOISE))
yf[target_idx] = 0

# 傅里叶逆变换
inv_yf = ifft(yf)

# 绘制处理后的信号波形图
plt.plot(t, inv_yf.real) # 取实部作为处理后的信号
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.title('Filtered Signal')
plt.show()