掌握Scipy优化运算

‌Scipy优化模块（scipy.optimize）用于解决各种数学优化问题，它提供了多种优化算法，具体包括：
‌无约束优化‌：寻找目标函数在不考虑限制条件下的最小值或最大值。
‌约束优化‌：在满足特定条件的前提下，找到目标函数的最优解。
‌全局优化‌：针对复杂的多峰函数，寻找全局最优解。
‌非线性最小二乘‌：用于拟合非线性模型到数据。

无约束优化算法

无约束优化问题是指只有优化目标，而不存在约束条件的问题。用数学模型可表示为：寻求多元函数f(x)的极小值点，其中x为n维实数空间Rn中的一个向量。这类问题在数据拟合、机器学习、控制理论等多个领域经常出现。
无约束优化常用算法包括：‌‌梯度下降法（Gradient Descent）‌、‌牛顿法（Newton's Method）‌、‌共轭梯度法（Conjugate Gradient Method）‌、拟牛顿法（Quasi-Newton Methods）等。
在选择无约束优化算法时，需要考虑问题的规模、数据的稀疏性、对计算精度的要求以及算法的收敛速度等因素。不同的算法在不同的场景下具有各自的优势和局限性。
例如，在机器学习中，对于大规模数据集和需要快速迭代更新的场景，通常会选择梯度下降法或其改进版本（如动量法、Adam算法等）。而对于需要高精度解的场景（如数值优化问题），则可能会选择牛顿法或拟牛顿法。
使用梯度下降法优化案例
假设我们要优化一个二次函数 f(x, y) = (x - 2)^2 + (y - 3)^2，这是一个简单的凸函数，其最小值在点 (2, 3) 处。

import numpy as np
from scipy.optimize import minimize

# 定义目标函数
def objective_function(x):
return (x[0] - 2)**2 + (x[1] - 3)**2

# 定义梯度函数
def gradient_function(x):
grad = np.zeros_like(x)
grad[0] = 2 * (x[0] - 2)
grad[1] = 2 * (x[1] - 3)
return grad

# 初始猜测
x0 = np.array([0.0, 0.0])

# 使用 minimize 函数进行优化，指定梯度函数
result = minimize(objective_function, x0, jac=gradient_function, method='BFGS')
# 注意：这里method='BFGS'是一个拟牛顿法，但我们可以利用jac参数传入梯度函数
# 实际上，对于简单的二次函数，我们可以直接使用'CG'（共轭梯度法），它更接近于纯梯度下降的一种变体，但这里为了展示如何使用梯度函数，我们仍然使用BFGS。
# 如果要更贴近梯度下降，可以选择'SGD'（随机梯度下降）的变种，但SciPy的minimize并不直接支持SGD，这通常需要在深度学习框架中实现。
# 不过，对于本例，我们可以忽略method参数的具体选择，因为重点是展示如何使用梯度函数。

# 打印优化结果
print("Optimal values:", result.x)
print("Optimal function value:", result.fun)

示例代码定义了gradient_function来计算目标函数的梯度。尽管上面的代码没有直接使用纯梯度下降法（因为SciPy的minimize函数没有提供直接的梯度下降实现），但它展示了如何使用自定义的梯度函数与SciPy的优化函数相结合来解决问题。对于更复杂的优化问题，这种方法同样适用。

约束优化算法

约束优化问题是在自变量满足约束条件的情况下目标函数最小化（或最大化）的问题。其中，约束条件既可以是等式约束，也可以是不等式约束。
约束优化通过将约束条件纳入优化模型，可以有效地解决实际问题中的复杂约束关系，从而提升决策的效率和准确性。例如，在生产调度问题中，约束优化算法可以求解具有线性或非线性目标函数和约束条件的生产计划，以最大化生产效率或最小化生产成本。在物流配送问题中，则可以求解具有车辆容量、时间窗等约束条件的配送路线规划问题，以最小化配送成本或时间。
求解带约束的最优化问题
假设我们要最小化的目标函数是：
f(x) = 0.5 * (x[0]^2 + x[1]^2)
约束条件：
3 * x[0] + 3 * x[1] + x[2] - 1 <= 0
4 * x[0] + 3 * x[1] + x[2] - 1 <= 0
-x[0] - x[1] - x[2] - 1 <= 0

示例代码

from scipy.optimize import minimize
import numpy as np

# 定义目标函数
fun = lambda x: 0.5 * (x[0]** 2 + x[1] **2)

# 定义约束条件
cons = ({'type': 'ineq', 'fun': lambda x: 3 * x[0] + 3 * x[1] + x[2] - 1},
{'type': 'ineq', 'fun': lambda x: 4 * x[0] + 3 * x[1] + x[2] - 1},
{'type': 'ineq', 'fun': lambda x: -x[0] - x[1] - x[2] - 1})

# 定义初始值
x0 = np.array([0, 0, 0])

# 使用minimize函数求解
res = minimize(fun, x0, method='SLSQP', constraints=cons)

# 输出结果
print('最小值:', res.fun)
print('最优解:', res.x)
print('迭代终止是否成功:', res.success)
print('迭代终止原因:', res.message)

输出：
最小值: 0.25000000000000056
最优解: [0.5 0.5 -2. ]
迭代终止是否成功: True
迭代终止原因: Optimization terminated successfully。

代码解读
定义约束条件时，type字段指定了约束的类型，ineq表示不等式约束，eq表示等式约束。minimize函数的method参数指定了求解算法，这里使用了SLSQP（顺序最小二乘编程）算法。Scipy还支持其他多种算法，如BFGS、L-BFGS-B等，使用者可以根据具体问题选择合适的算法。初始值x0的设定对算法的收敛性和求解结果有重要影响，因此在实际应用中需要谨慎选择。

全局优化算法

全局优化算法是在一定约束条件下寻求优化问题的全局最优解或近似全局最优解。

全局优化算法案例
假设我们有一个复杂的多峰函数，目标是找到它的全局最小值。多峰函数是指具有多个局部最小值的函数，这使得局部优化算法难以找到全局最小值。因此，我们需要使用全局优化算法来搜索整个参数空间，并找到全局最优解。

示例代码

import numpy as np
from scipy.optimize import differential_evolution
import matplotlib.pyplot as plt

#定义目标函数
def multimodal_function(x):
# 添加一些噪声使函数更复杂
return np.sin(x) + 0.1 * np.random.randn()

#绘制函数图像
x_values = np.linspace(-10, 10, 1000)
y_values = multimodal_function(x_values)
plt.plot(x_values, y_values, label='Multimodal Function')
plt.legend()
plt.title('Multimodal Function')
plt.show()

# 定义搜索范围
bounds = [(-10, 10)]

# 使用differential_evolution进行全局优化
result = differential_evolution(multimodal_function, bounds)

# 打印全局最小值及其对应的x值
print(f'Global Minimum: {result.fun} at x = {result.x}')

运行示例代码后，differential_evolution函数将返回全局最小值及其对应的x值。由于目标函数中添加了噪声，所以每次运行代码时得到的结果可能会有所不同。但是，通过多次运行并比较结果，可以发现differential_evolution函数能够稳定地找到全局最小值附近的解。

非线性最小二乘

非线性最小二乘法是一种重要的参数估计方法，它通过最小化误差平方和来估计非线性模型的参数。模型通常表示为y=f(x,θ)，其中y是系统的输出，x是输入，θ是参数（它们可以是向量）。这里的非线性是指对参数θ的非线性模型，不包括输入输出变量随时间的变化关系。
在估计参数时，模型的形式f是已知的。通过N次实验取得数据(x1,y1),(x2,y2),…,(xn,yn)，然后选择一个准则（或称目标函数）来评估模型的好坏。这个准则通常选为模型的误差平方和。非线性最小二乘法的目标就是找到使误差平方和达到极小的参数估计值θ。

非线性最小二乘法案例
假设有一组实验数据，数据包括自变量x和因变量y。我们希望找到一个非线性函数来拟合这些数据，并估计该函数的参数。

示例代码

import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

# 准备实验数据
# 自变量x
x_data = np.array([1, 2, 3, 4, 5])
# 因变量y，假设这些数据带有一些噪声
y_data = np.array([2.1, 3.8, 6.5, 9.2, 11.9])

# 定义非线性模型函数
# 假设模型函数为 a * (x**2) + b * x + c
def func(x, a, b, c):
return a * (x**2) + b * x + c


# 调用curve_fit函数进行拟合
popt, pcov = curve_fit(func, x_data, y_data)

# 分析拟合结构
# 获取拟合的参数值
a_fit, b_fit, c_fit = popt

# 计算拟合值
y_fit = func(x_data, a_fit, b_fit, c_fit)

# 计算均方根误差（RMSE）
rmse = np.sqrt(np.mean((y_data - y_fit)**2))

print("拟合结果:")
print("a =", a_fit)
print("b =", b_fit)
print("c =", c_fit)
print("RMSE =", rmse)

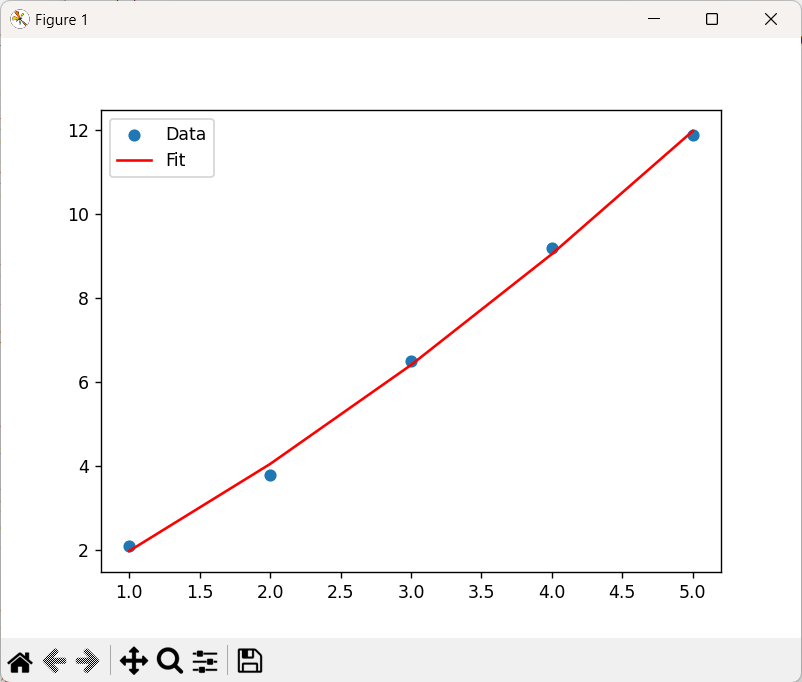
拟合结果如下图所示：