NumPy矩阵运算:求解线性方程组
- NumPy矩阵运算
- 2024-10-14
- 694热度
- 0评论
矩阵与线性方程组
将类似于“2x + 3y = 1”这样的等式放在一起,并找出满足所有等式的x和y的值,就构成了线性方程组。
如下面的线性方程组:
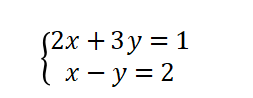
求解该线性方程组的几何意义是:
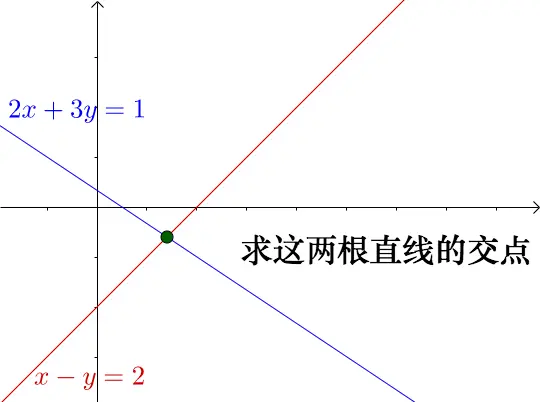
解的情况分为以下三种:
两条直线相交于一点,此时方程组有一个解。
两条直线共线,即它们完全重合,这种情况下方程组有无数解。
两条直线平行,互不相交,此时方程组无解。
若从矩阵与向量的视角审视此问题,将会开启一种全新的解题思路。
可以把上面方程组的系数、未知数、常数用矩阵的方式来表示,这样求解线性方程组的问题就转换为矩阵运算的问题。
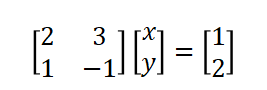
设系数矩阵为A,未知数为向量x,常数为向量b,则得到了更一般的形式:
Ax = b
这样就转换成了我们熟悉的Ax=b矩阵的乘法形式,求解向量x。解线性方程组问题就转化为空间映射问题,已知目标空间的向量b,和描述空间映射的矩阵A,去求解位于原空间映射过来的向量x。
如果方程组有解,满足Ax=b等式成立,向量b就是矩阵A各列与向量x的线性组合,因此向量b只有在矩阵A与向量A线性组合的列空间上,才能满足方程组有界。
使用NumPy解线性方程组
在Python的NumPy库中,求解线性方程组通常使用numpy.linalg.solve函数。给定一个线性方程组Ax = b,其中A 是一个系数矩阵,b 是一个常数向量,numpy.linalg.solve可以求解出未知数向量 x。
下面是一个使用numpy.linalg.solve求解线性方程组的示例:
# 导入NumPy库
import numpy as np
# 定义一个二维数组A,作为线性方程组的系数矩阵
# 这个例子中的方程组可以表示为:
# 2x + 3y = 1
# 1x - 1y = 2
A = np.array([[2, 3], [1, -1]])
# 定义一个一维数组b,作为线性方程组的常数项向量
# 即方程组右侧的值
b = np.array([1, 2])
# 使用NumPy的线性代数模块(linalg)中的solve函数来求解线性方程组Ax = b
# 这里,x是我们要找的解向量,使得A乘以x等于b
x = np.linalg.solve(A, b)
# 打印解向量x
# 对于这个特定的方程组,解应该是x和y的值,分别对应于x数组中的元素
print("解向量x:", x)
# 输出结果将是方程组的一个解,比如x和y的值,这取决于系数矩阵A和常数项向量b的具体值
这段代码首先通过np.array创建了两个NumPy数组:一个二维数组A作为线性方程组的系数矩阵,和一个一维数组b作为方程组的常数项。然后,它使用np.linalg.solve函数来求解这个线性方程组,找到满足Ax = b的x向量,并打印出解向量x。
需要注意的是,numpy.linalg.solve函数要求系数矩阵A必须是方阵,并且是可逆的(即,矩阵的行列式不为0)。如果A不是方阵或者不可逆,这个函数将会抛出异常。对于非方阵系统,可以使用numpy.linalg.lstsq函数求解最小二乘解。
求解线性方程组应用案例
假如猪肉、牛肉、鸡蛋的价格在一周内不发生变化,记录近三周内的价格。为计算简单起见,价格都设定为整数。
| 猪肉 | 牛肉 | 鸡蛋 | |
| 第一周 | 15 | 28 | 5 |
| 第二周 | 12 | 31 | 6 |
| 第三周 | 13 | 29 | 7 |
设某个家庭每周对猪肉、牛肉、鸡蛋的需求分别为4千克、3千克、2千克,求这个家庭近三周对上述三种食品的需求开支?
一般计算过程为:
第一周:15 X 4 + 28 X 3 + 5 X 2 = 154
第二周:12 X 4 + 31 X 3 + 6 X 2 = 153
第三周:13 X 4 + 29 X 3 + 7 X 2 = 153
现在把上面的数据用矩阵来表示,矩阵A表示猪肉、牛肉、鸡蛋三周的价格,矩阵B表示某个家庭每周的需求。
下面用线性方程组求解。
设某家庭近三周每周对猪肉、牛肉、鸡蛋的需求分别为x千克、y千克、z千克,已知近三周每周猪肉、牛肉、鸡蛋的价格和某家庭近三周每周的消费,求x、y和z。
可以列三元一次方程组:
15x + 28y + 5z = 154
12x + 31y + 6z = 153
13x + 29y + 7z = 153
可以把上面方程组的系数、未知数、常数用矩阵的方式来表示,这样就可以使用矩阵运算来求解方程组。
求解三元一次方程组的问题就变为:
已知A矩阵,已知A矩阵和B矩阵的乘积C矩阵,求B矩阵的问题。Numpy库的 linalg模块的solve()函数可以使用矩阵求解线性方程组。
# 导入numpy库
import numpy as np
# 程序入口
if __name__ == '__main__':
# 建立3X3矩阵
ta = np.array([[15,28,5],
[12,31,6],
[13,29,67]
])
# 建立3维行向量
tb = np.array([154,153,153])
# 解线性方程组
x = np.linalg.solve(ta,tb)
# 输出x、y、z的值
print("x = %.2f y = %.2f z = %.2f" % (x[0],x[1],x[2]))