数据图表：刀具磨损回归分析案例

【摘要：课程通过刀具磨损回归分析案例，借助于EXECL分析工具，讲述数据分析的结果表达——数据图表的使用，重点讲述了回顾分析结果的散点图、趋势线和回归统计表，并编写Python程序绘制散点图和趋势线。】
数据图表直观易懂，因此数据分析结果一般采用数据图表来表示。
下面是一组测试刀具磨损速度的数据， 测试过程为每隔1小时，测量一次刀具的厚度，得到下面一组实验数据：

设时间为t，刀具厚度为为y，根据上面的数据建立时间t和刀具厚度y之间的函数关系y=f(t)，对数据进行线性回归分析。

我们使用EXECL对上述数据进行回归分析，EXECL版本是2016，具体步骤：

（1）选择要分析的数据，如下图所示：

（2）展开【数据】标签栏，在【数据】标签栏中选择“数据分析”功能，如下图所示：

若【数据】标签栏内没有数据分析功能，需要安装“分析工具库”，依次选择【文件】->【更多】->【选项】，出现下面的对话框：

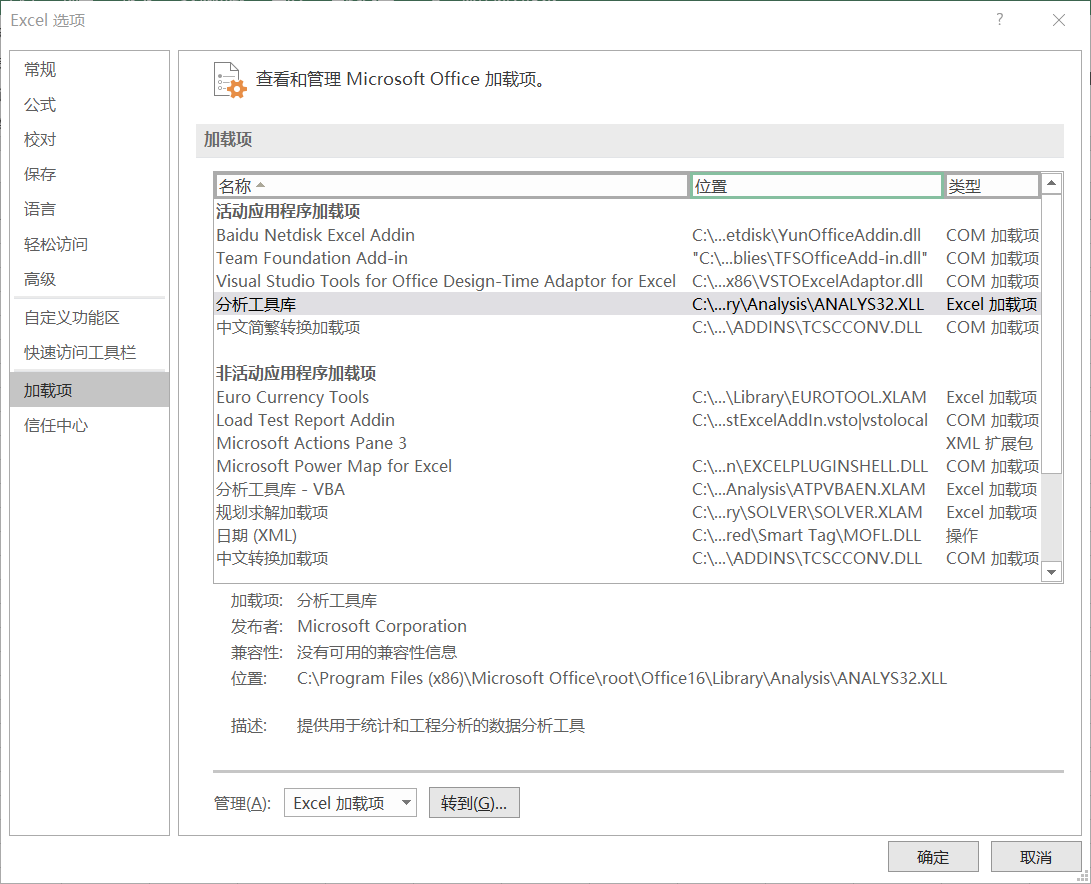
在对话框左侧选择“加载项”命令，在对话框右侧选择“分析工具库”，单击“确定”按钮即可安装“分析工具库”。

（3）在数据分析对话框，选择回归分析，如下图所示：

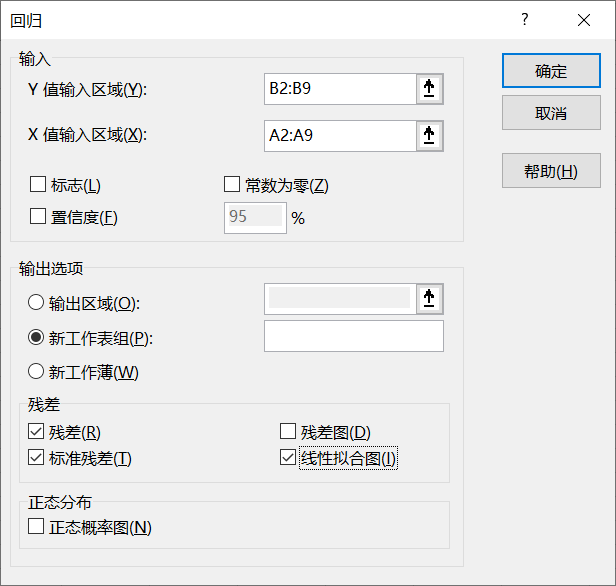
（4）在回归分析对话框，填入需要进行回归分析的数据区域和输出选项。X值输入区域为时间数据，Y值输入区域为刀具厚度数据。输出的图表选择残差、线性拟合图和标准残差。

（5）回归分析结果的数据图表会出现在新工作表组：

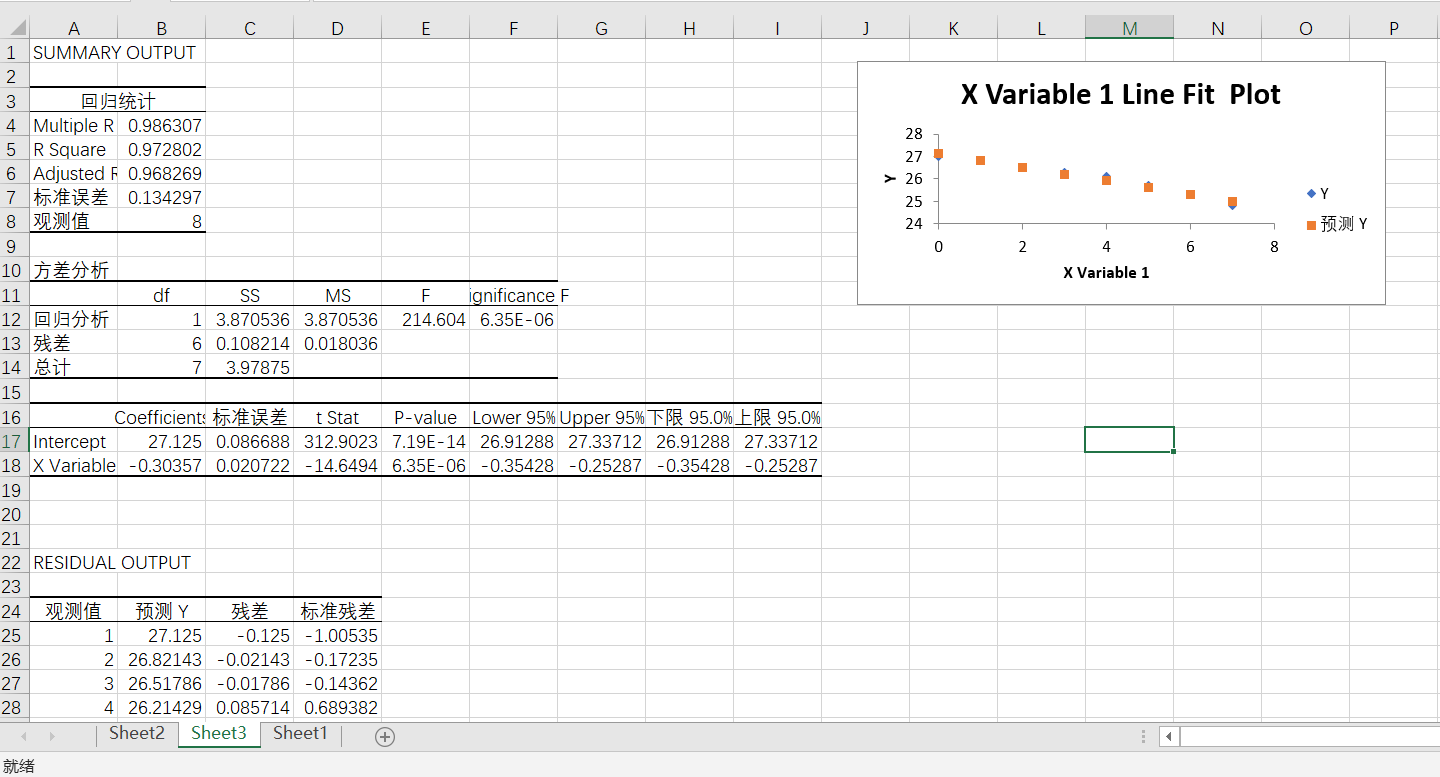
（6）观察EXECL给出的分析图表，并没有给出与数据关系近似的线性函数。选择散点图，单击散点图右侧的“+”按钮，添加趋势线，并设置趋势线格式，在“设置趋势线格式”窗口，选择“选中公式”选项。趋势线和趋势线函数会显示在散点图内。

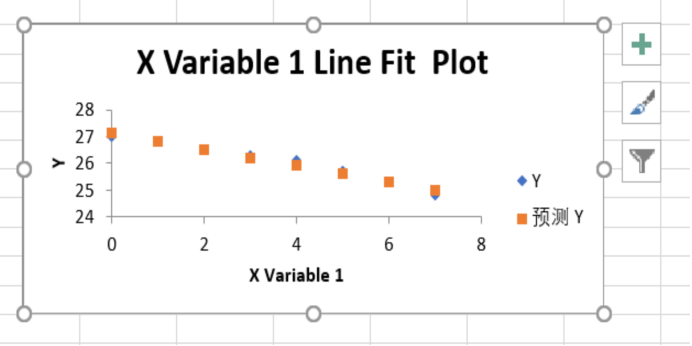
至此，我们通过EXECL完成了对刀具磨损数据的线性回归分析，下面观察回归分析结果数据图表，看看我们通过数据图表能够获取哪些信息。

观察散点图

散点图给出了刀具厚度（y）随时间（x）变化的大致趋势，散点图内显示的函数是拟合散点数据点的线性函数，黄色的点是通过函数预测的刀具厚度（y），也称为预测值，蓝色的点是实际测试的刀具厚度（y），也称为经验值。直观上看，函数可以很好反映刀具厚度随时间变化的趋势，通过函数可以预测未来时间内刀具厚度的变化。

下面编写Python程序来绘制散点图和趋势线：

# 导入matplotlib库
import numpy as np
# 导入matplotlib库
import matplotlib.pyplot as plt

# 定义绘制趋势线函数
# x,y为实验数据，n表示n次函数
def plot_trendline(x,y,n):
    # 计算实验数据的拟合函数系数
    z = np.polyfit(x,y,n)
    # z为拟合函数系数向量，返回拟合函数
    p = np.poly1d(z)
    # 绘制拟合函数图形
    # r--为红色点划线
    plt.plot(x,p(x),"r--")
   

# 定义实验数据
x = [0,1,2,3,4,5,6,7]
y = [27,26.8,26.5,26.3,26.1,25.7,25.3,24.8]
# 设置散点图标量和颜色
plt.scatter(x,y, s=40, c='green')

# 设置散点图标题
plt.title("X Variable 1 Line Fit  Plot", fontsize=20)
# 设置散点图x轴标题
plt.xlabel("X Variable 1", fontsize=16)
# 设置散点图y轴标题
plt.ylabel("Y", fontsize=16)
plot_trendline(x,y,1)
#显示绘制的图形
plt.show()

程序执行后输出结果如下图所示：

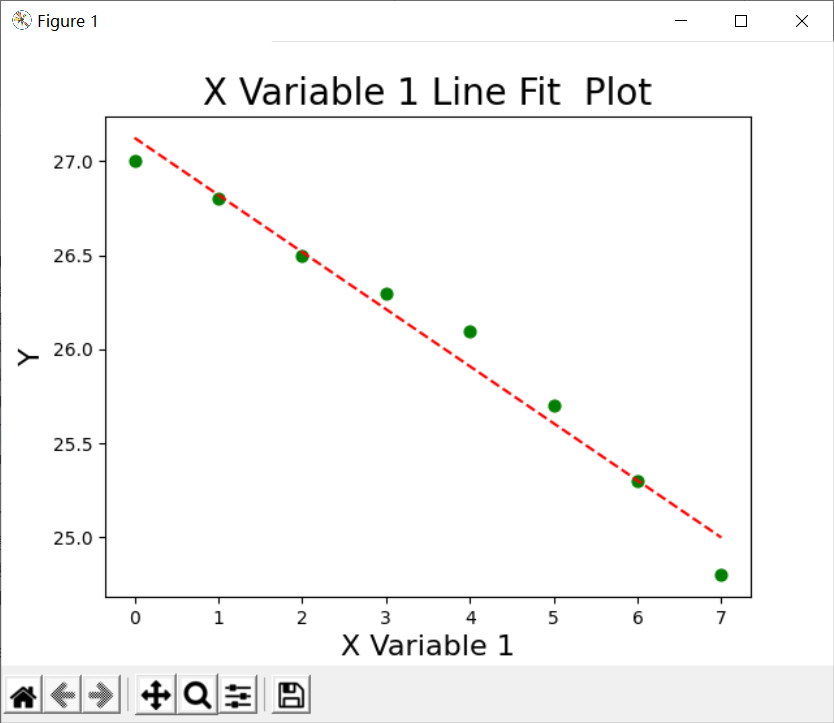
观察回归统计表

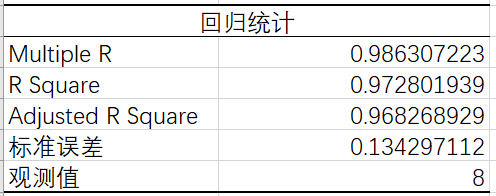
Multiple R是刀具厚度（y）和时间（x）的相关系数，该值一般在-1~1之间，该值为正数时为正相关，为负数时为负相关，为0时没有相关性。该值越接近于1，说明x和y正相关越强，该值越接近于-1，说明负相关越强。

在回归与相关分析中，因变量值随自变量值的增大（减小）而减小（增大），在这种情况下，因变量和自变量的相关系数为负值，即负相关。

观察散点图的趋势线发现，时间（x）和刀具厚度（y）应该是负相关，EXECL回归统计表给出的是正相关，应该是忽略了正负相关性。

相关系数的计算公式如下：

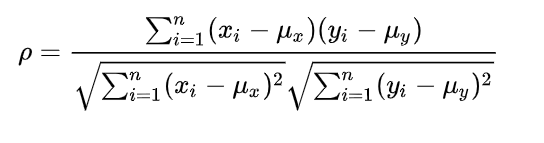
相关系数ρ是一个比值，分子是实验数据中的每个数据点的x和y，分别与期望值之差乘积的累加和，分母是每个实验数据点的x和y，分别与期望值之差平方后累加和再开方的乘积。

相关系数可以直接编写Python程序计算出来，当然也可以手动计算，数据分析工具Pandas提供了计算相关系数的方法。

# 导入pandas库
import pandas as pd

# 定义DataFrame数据列
df = pd.DataFrame({'time':[0,1,2,3,4,5,6,7],
   'thick':[27,26.8,26.5,26.3,26.1,25.7,25.3,24.8]})

# 输出DataFrame数据列
print(df)
# 计算DataFrame数据列的相关系数
print(df.corr())

程序执行后，输出结果如下图所示：

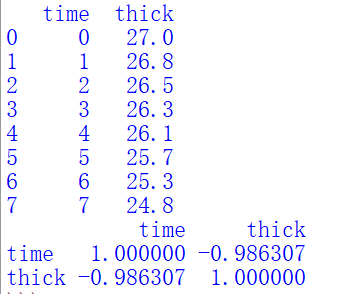
观察输出结果发现，time与thick的相关系数为-0.986307，时间（x）和刀具厚度（y）应该负相关，相关性接近于-1，说明x和y的关系近似于线性函数。

R Square为线性函数的确定系数，用于衡量线性回归模型（近似的线性函数），预测因变量随自变量变化的可靠程度。该值一般在0~1之间，该值越接近于1，说明回归分析给出的回归模型更可靠。R Square的值为相关系数的平方。

Adjusted R Square用于校正确定系数，Adjusted R Square的计算公式为：

1-(n-1)(1-r)/(n-p-1)

其中n是样本数量（实验数据的个数），p是模型中变量的个数（实验数据近似线性函数变量的个数，近似线性函数也称为模型），r是R Square。

Adjusted R Square主要是考虑模型中变量的增加对模型拟合度（线性函数对实验数据的拟合程度）的影响，在模型中添加新的变量，模型会变得复杂，R Square的值会变大，貌似模型的的拟合度会更优（有可能这是表明现象），若Adjusted R Square没有相应提高，说明增加变量后模型的拟合度并不高于原来模型的拟合度。

总的来说，如果两个模型，样本数一样，R Square一样，那么从校正R Square的角度看，使用变量个数少的那个模型更优。

标准误差是预测值与实验数据偏差的平方与样本数量n-2比值累加和的平方根，计算公式为：

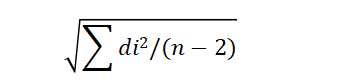
其中，di为一组预测值值与实验值的偏差，i=1,2,3,……,n，n为样本数量，在计算标准误差中，n-2是指自由度。

在EXECL给出的方差分析表中，df栏就是回归分析模型的自由度。自由度为当总体由样本估计时，样本中独立或自由变化的数量。回归分析的自由度为1，说明回归模型只有一个变量，该变量对应样本中的刀具厚度（y）。在回归分析中，总的自由度为样本数量减1，残差的自由度为总的自由度减1。

因此标准误差是预测值与实验数据偏差的平方与残差自由度比值累加和的平方根。

方差分析表的其它数据项，请读者自行查阅相关资料。