应用Python绘制动态曲线，直观展示指数级增长与复利思维

指数增长VS线性增长和幂增长

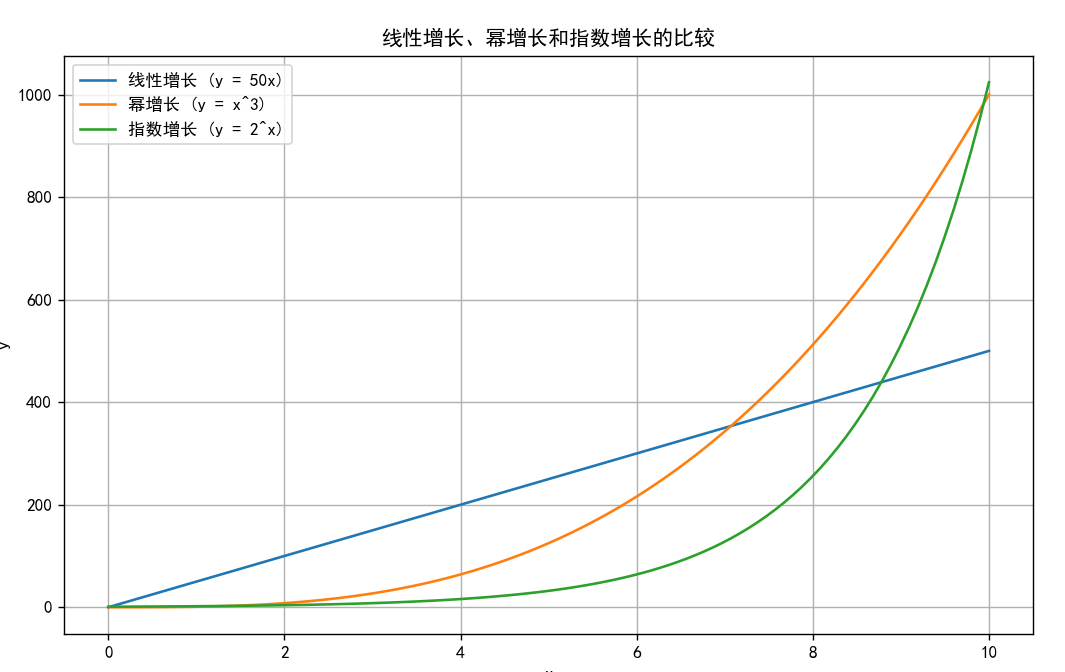
随着变量的增加，指数增长的速度非常快，比线性增长和幂增长都要快得多。就像图上展示的，绿色的曲线（指数增长）很快就超过了蓝色的曲线（线性增长）和橙色的曲线（幂增长）。但是，在开始的时候，指数增长的值很小，所以很容易被其他两种增长方式盖住，人们可能不太会注意到它的重要性，或者低估了它。

对编程感兴趣的读者可以尝试使用Python语言来绘制上面的图形，Python代码如下：

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为宋体
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 设定x的范围
x = np.linspace(0, 10, 100) # 从0到10，共100个点

# 定义增长曲线参数
# 线性增长: y = 50x
a_linear = 50
y_linear = a_linear * x

# 幂增长: y = x^3
b_power = 3
y_power = np.power(x, b_power)

# 指数增长: y = 2^x
y_exp = np.power(2, x)
# 绘制曲线
plt.figure(figsize=(10, 6))

plt.plot(x, y_linear, label='线性增长 (y = 50x)')
plt.plot(x, y_power, label='幂增长 (y = x^3)')
plt.plot(x, y_exp, label='指数增长 (y = 2^x)')

# 设置图例
plt.legend()

# 设置标题和坐标轴标签
plt.title('线性增长、幂增长和指数增长的比较')
plt.xlabel('x')
plt.ylabel('y')
# 显示图表
plt.grid(True) # 显示网格线
plt.show()

指数增长的滚雪球效应

细胞分裂是一个很好的指数级增长案例。在理想情况下，一个细胞在每次分裂时都会变成两个完全相同的细胞。如果我们从一个细胞开始，并且每次分裂都产生两个新的细胞，那么细胞的数量就会随着分裂次数的增加而呈指数增长。
假设我们开始时有一个细胞，并且每过一定的时间（比如一个小时）细胞就会分裂一次。我们可以用指数函数来描述细胞数量的增长。
设 t 为时间（以小时为单位），N(t) 为 t 小时后细胞的数量。因为每次分裂细胞数量翻倍，所以底数为 2。初始时（t=0）有一个细胞，所以指数为 t。因此，细胞数量随时间变化的函数可以表示为：

N(t) = 2^t
我们编写一个简单的Python，计算并打印出不同时间点的细胞数量。

# 定义一个函数来计算细胞数量
def cell_count(t):
return 2 ** t
# 打印出不同时间点的细胞数量
for t in range(10): # 假设我们观察10个小时内的细胞数量
print(f"经过 {t} 小时后，细胞数量为：{cell_count(t)} 个")

运行这段代码，当时间t愈来愈大时，你会看到细胞数量如何随着时间的推移而呈指数级增长。
具体地说，如果我们从单个细胞开始，并假设每个细胞分裂周期（例如，一天）后都会分裂成两个，那么我们可以这样计算细胞数量的增长：
初始时（第0天），有1个细胞。
第1天后，有2个细胞（1 * 2^1）。
第2天后，有4个细胞（1 * 2^2）。
第3天后，有8个细胞（1 * 2^3）。 ... n天后，有 2^n 个细胞（其中n是天数，从0开始计数）。
这种增长方式就是指数级增长。它的特点是增长速度越来越快，因为每次分裂都会翻倍。因此，即使开始时的数量很少（只有一个细胞），在经历几个分裂周期后，数量也会变得非常庞大。
下面我们来编写一个Python程序，使用动画来演示细胞分裂的指数级增长。

# 导入必要的库
import numpy as np # NumPy库用于数值计算
import matplotlib.pyplot as plt # Matplotlib库用于绘图
from matplotlib.animation import FuncAnimation # 用于创建动画
import matplotlib as mpl # Matplotlib的配置和设置

# 设置matplotlib的后端为TkAgg，以便在某些环境下能够正常显示图形
mpl.use('TkAgg')

# 确保当前环境没有已打开的图形窗口，如果有则关闭它
if os.environ.get('DISPLAY','') == '':
print('No display found. Using non-interactive Agg backend')
mpl.use('Agg')

# 创建一个图形和坐标轴
fig, ax = plt.subplots()

# 初始化xdata和ydata为空列表，用于存储动画的x和y数据
xdata, ydata = [], []

# 创建一个空的红色圆点线
ln, = plt.plot([], [], 'ro')

# 初始化函数：设置坐标轴的范围
def init():
ax.set_xlim(0, 20) # 设置x轴的范围为0到20
ax.set_ylim(0, 30000) # 设置y轴的范围为0到30000
return ln, # 返回需要更新的图形元素

# 更新函数：用于每一帧的更新
def update(frame):
xdata.append(frame) # 将当前帧数添加到xdata中
ydata.append(2**frame) # 计算2的frame次方，并添加到ydata中
ln.set_data(xdata, ydata) # 更新线的数据
return ln, # 返回需要更新的图形元素

# 创建动画
# frames参数指定了帧数，即update函数会被调用的次数
# init_func参数指定了初始化函数
# blit参数为True时，仅更新需要更新的部分，提高性能
ani = FuncAnimation(fig, update, frames=20,
init_func=init, blit=True)

# 保存动画为GIF文件
ani.save('exp.gif')
# 显示图形
plt.show()

动画效果如下所示：

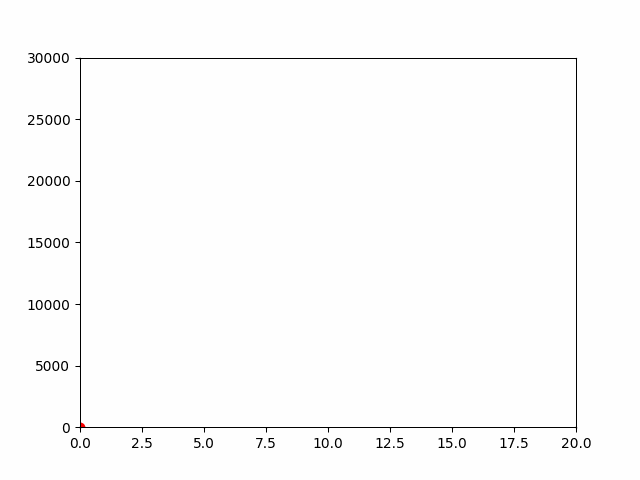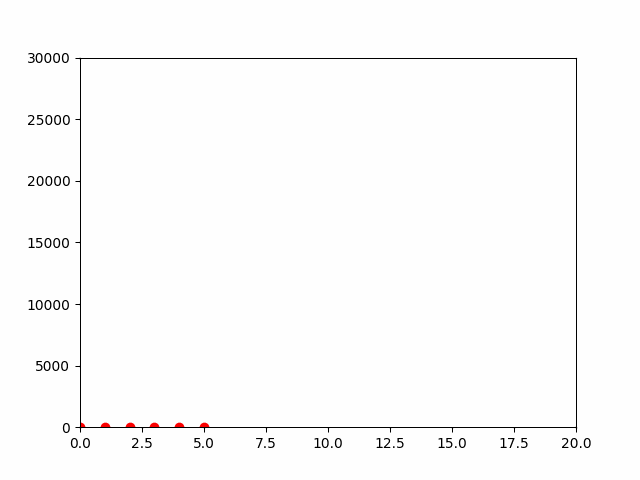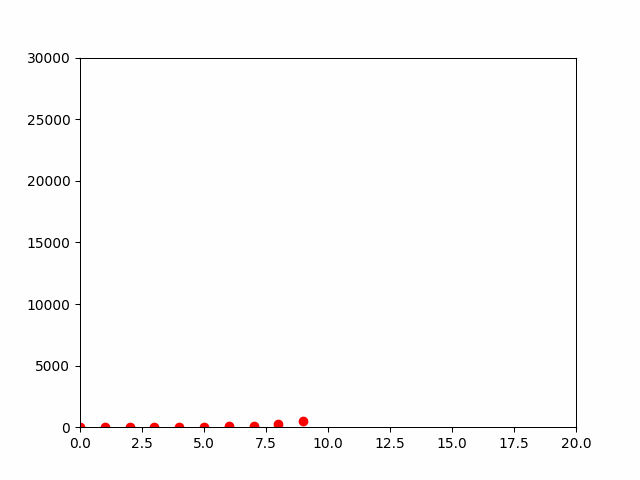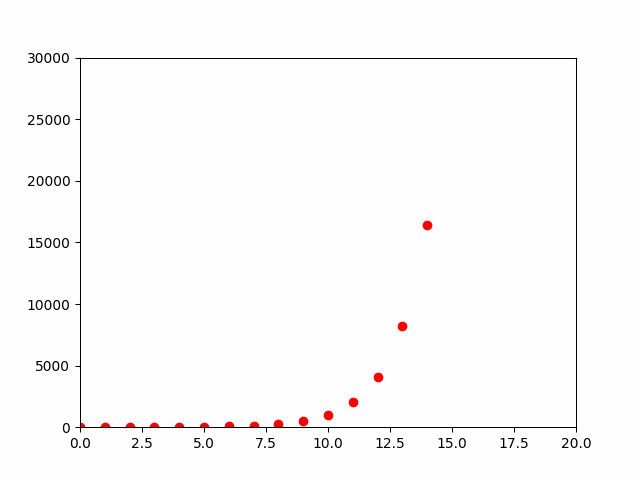
指数级增长在初期，增长可能并不显著，类似于线性增长。然而，随着时间的推移，指数级增长的威力逐渐显现，增长速度显著加快。在投资、股票等领域，这种现象常被比喻为“滚雪球效应”，意味着随着操作的进行，投资者所能获得的收益不断增长。

舍罕王无法兑现的承诺

舍罕王的失算（又称棋盘上的麦粒）也是一个典型的指数级增长问题的例子。舍罕王是古印度的一个国王，他喜欢上了下棋，并且和大臣达依尔下棋时输给了他。达依尔请求国王赏赐他麦子，要求是棋盘的第一个格子放1粒麦子，第二个格子放2粒，第三个格子放4粒，第四个格子放8粒，以此类推，每个格子放的麦子是前一个格子的两倍，直到放满整个64格的棋盘。国王觉得要求很简单，就答应了。但是，当真正开始计算所需的麦子数量时，国王才发现这是一个天文数字，他无法兑现这个承诺。

这个问题可以通过数学公式来解决：
总麦粒数 = 1 + 2 + 4 + 8 + ... + 2^(63)
这是一个等比数列的求和问题，其中首项是1，公比是2，项数是64。使用等比数列的求和公式，可以得到：
总麦粒数 = (1 - 2^64) / (1 - 2) = 2^64 - 1
2^64这个数有多大呢？
想象一下，你有足够多的米粒（像沙子那么小）来填满一个标准的足球场，每一粒米都紧紧挨着没有空隙。那么，2^64 粒米将远远超过这个数量，多到几乎无法用我们日常的经验去想象。
具体来说，2^64 等于 18,446,744,073,709,551,616 粒米。这意味着如果你有这么多粒米，你可以：
铺满整个地球表面，并且米粒之间的间距小于人类头发的直径。
给全世界的每个人分配数百万粒米，并且还剩下很多。
用这些米堆起来，其高度将超过地球到月球的距离。
它是计算机能够直接处理的极限大小之一（当然，有更大的数据类型，但 64 位整数是常见的），也是许多算法和数据结构在设计和分析时需要考虑的重要因素。

复利思维

在有限的时间，把有限的精力和财富，持续而反复地投入到某一领域，长期坚持下去，最终产生的积极影响，会如雪球越滚越大，它带来的回报一定超过你的想象。这就是经济学中典型的复利思维。
复利是金融学中的一个重要概念，它描述了一种特殊的利息计算方式，即利息不仅在本金上产生，而且在利息本身上也能产生利息。这种计算方式导致资金随时间呈现指数级增长。
复利的计算公式为：
F=P*(1+i)^n
其中F表示终值，P表示本金，i表示利率，n表示计息期数。
例如，如果你投资了 1000 元，年利率为 5%，投资期限为 3 年，那么根据复利原则，3 年后的最终价值 F 可以这样计算：
F = 1000 * (1 + 0.05)^3 = 1000 * 1.157625 = 1157.63 元
这意味着，3 年后，你的投资将从 1000 元增长到大约 1157.63 元。
在复利计算中，每一期的利息都会计入下一期的本金中，从而产生新的利息。这种计算方式使得资金随时间呈现出指数级的增长趋势。
我们来看这笔投资的动态增长曲线。

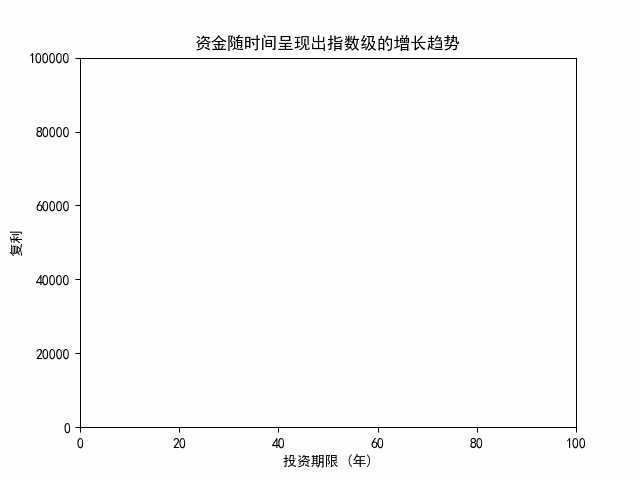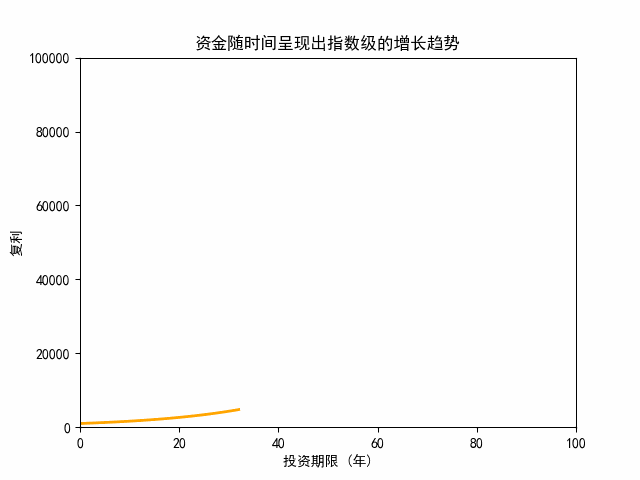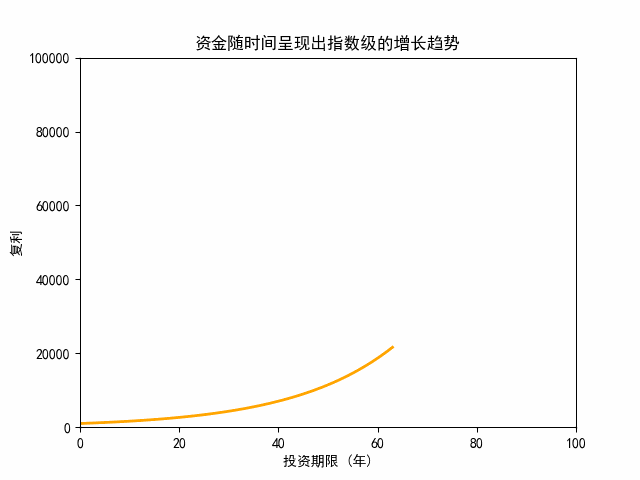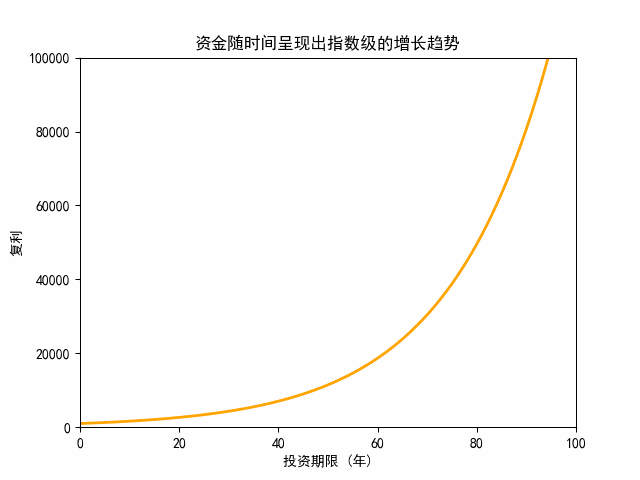
从动态曲线图可以看出，投资收益前60年增长缓慢，60年之后出现显著增长。
对编程感兴趣的读者可以尝试使用Python语言来绘制上面的动态曲线，Python代码如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体为宋体
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

# 定义初始参数
principal = 1000 # 本金
rate = 0.05 # 年利率
periods = 100 # 期数（年份）

# 创建一个时间数组
time = np.arange(periods)

# 定义一个函数来计算复利
def compound_interest(principal, rate, time):
return principal * (1 + rate) ** time

# 初始化复利数组
compound_interests = compound_interest(principal, rate, time)

# 创建一个图形和轴
fig, ax = plt.subplots()

# 初始化线条
line, = ax.plot([], [], color='orange',lw=2)

# 初始化函数：设置坐标轴的范围
def init():
ax.set_xlim(0, 100) # 设置x轴的范围为0到20
ax.set_ylim(0, 100000) # 设置y轴的范围为0到30000
return line, # 返回需要更新的图形元素


# 设置轴标签和标题
ax.set_xlabel('投资期限 (年)')
ax.set_ylabel('复利')
ax.set_title('资金随时间呈现出指数级的增长趋势')

# 创建一个更新函数，该函数将在每个动画帧上调用
def update(frame):
# 更新线条的数据
line.set_data(time[:frame], compound_interests[:frame])
# 返回线条和可能需要的任何其他艺术家
return line,

# 创建一个动画
ani = FuncAnimation(fig, update, frames=periods, init_func=init,interval=200, blit=True)

# 保存动画为GIF文件
ani.save('compound.gif')

# 显示动画
plt.show()