快速理解树结构

郎哥
算法
2024-05-30
206热度
0评论

树结构的概念

想象一下，你站在一棵大树下，抬头望去，看到的是茂密的树枝和树叶。这些树枝和树叶是怎么分布的呢？它们就像是一个个节点，从树干这个根节点开始，一层一层地向上生长，分叉，再生长，再分叉。这就是树结构的基本形态。

图 2-15树的形态

树结构的特点在于它的层次性和分支性。每个节点都有自己的层级，就像树的层次一样。而且，每个节点都可以有自己的子节点，就像树枝可以分出更多的树枝一样。

树结构是一种非常重要的数据结构，在计算机科学中广泛应用，它是一种一对多的非线性结构，由n（n>=0）个有限结点组成一个具有层次关系的集合。把它称为树结构是因为它看起来像一棵根朝上叶朝下倒挂的树。

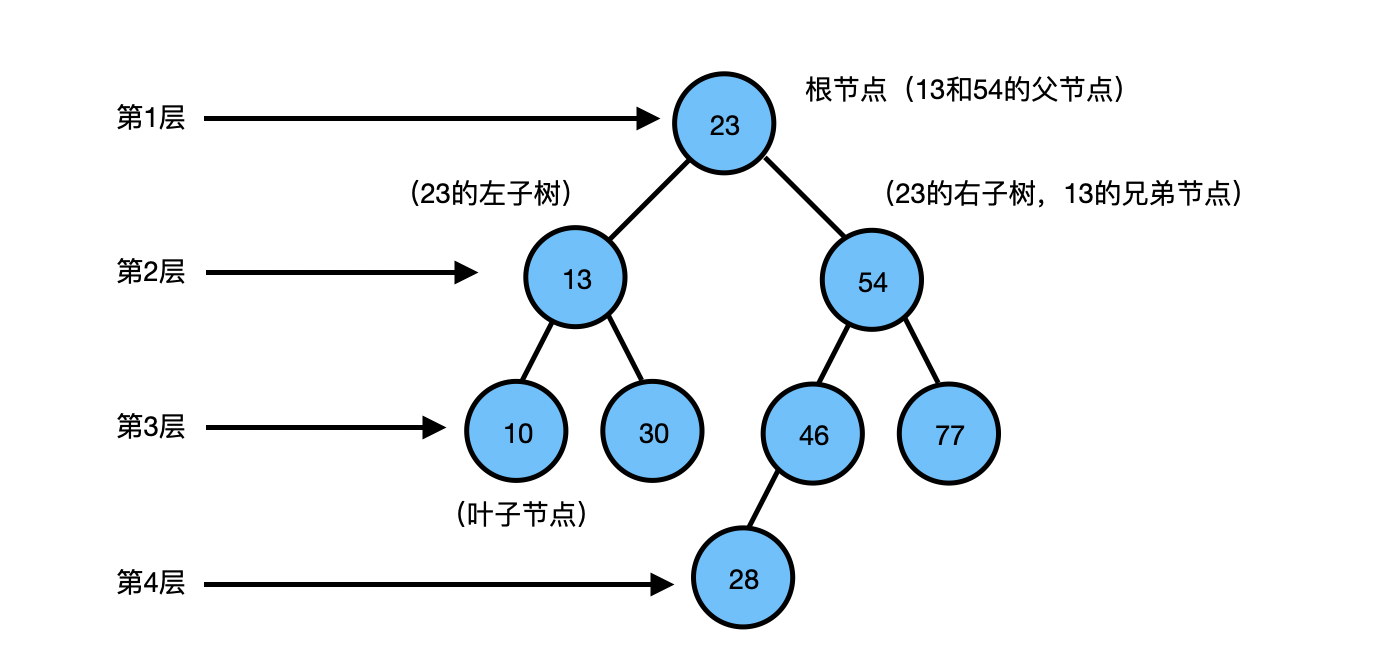
图 2-16 树结构图

根节点：一棵树最上面的节点称为根节点，如图中的23节点；

父节点、子节点：如果一个节点下面连接多个节点，那么该节点称为父节点，它下面的节点称为子节点，如图中的23节点是父节点，13和54为子节点；

叶子节点：没有任何子节点的节点称为叶子节点，如图中的10、30、77、28节点；

兄弟节点：具有相同父节点的节点互称为兄弟节点，如图中的13和54、10和30、46和47；

节点度：节点拥有的子节点数。图中13的度为2，46的度为1，28的度为0；

树的深度：从根节点开始（其深度为0）自顶向下逐层累加。图中13的深度是1，30的深度是2，28的深度是3；

树的高度：从叶子节点开始（其高度为0）自底向上逐层累加。54的高度是2，根节点23的高度是3；

对于树中相同深度的每个节点来说，它们的高度不一定相同，这取决于每个节点下面的叶子节点的深度。上图中，13和54的深度都是1，但是13的高度是1，54的高度是2。

树的基本定义

树是由n（n>=0）个节点组成的有限集合。如果n=0，则称为空树。如果n>0，则树满足以下两个条件：有且仅有一个特定的称为根（Root）的节点，其余节点可分为m（m>=0）个互不相交的有限集T1,T2,T3,...,Tm，其中每一个集合本身又是一棵树，并称为根的子树（SubTree）。

树的存储结构

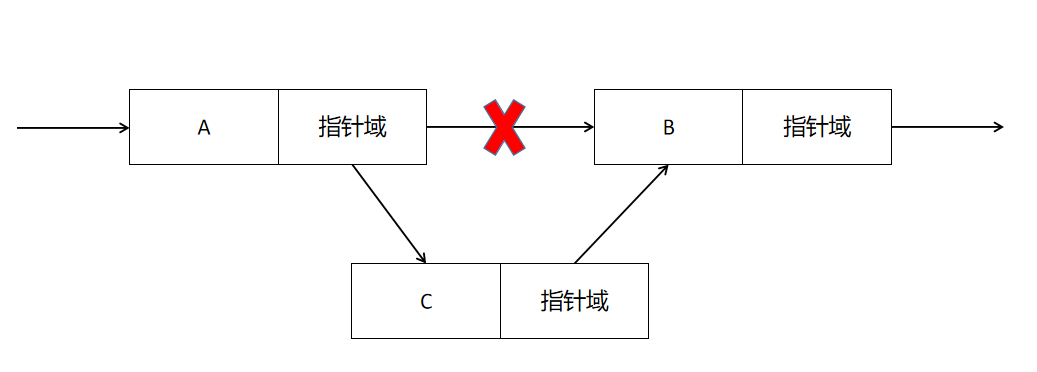
存储树结构有两种方式：顺序存储和链式存储。顺序存储通常用于存储线性数据结构，如数组和线性表，树结构为非线性，采用顺序存储会浪费大量的存储空间、也不利于树节点的插入、删除和查询。因此树结构一般采用链式存储。

链式存储的基本思想是通过指针或引用，将树中的节点连接起来。每个节点除了保存自身的数据外，还保存了指向其子节点的指针。通过这种方式，可以从根节点出发，沿着指针遍历整棵树。

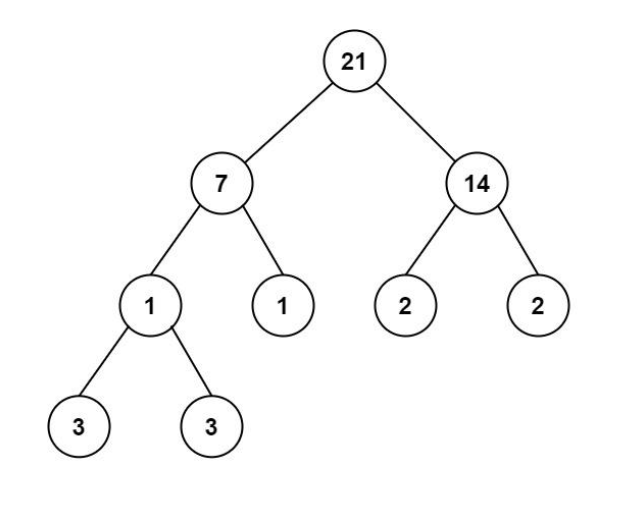
图 2-17二叉树

图2-3是一棵二叉树，二叉树是每个节点最多有两个节点的树结构，通常子节点被称作“左子树（当前节点左侧的子节点）”和“右子树（当前节点右侧的子节点）”。要存储图2-3的二叉树，需要定义一个结构体，结构体至少包含三个成员：一个数据成员和两个指针成员，分别指向左子节点和右子节点。

// 定义二叉树节点的结构体
typedef struct TreeNode {
    int data;          // 节点的值
    struct TreeNode* left;   // 左子节点的指针
    struct TreeNode* right;  // 右子节点的指针
}

往二叉树插入节点时，需要判断二叉树是否为空，如果树为空，则创建新节点作为根节点。否则，函数会比较新节点的值和当前节点的值，并决定是将新节点插入到左子树还是右子树。如果值已经存在于树中，则不插入新节点。

// 向二叉搜索树中插入节点
TreeNode* insertNode(TreeNode* root, int data) {
    // 如果树为空，则创建新的根节点
    if (root == NULL) {
        return createNode(data);
    }
    // 否则，递归地决定插入位置
    if (data < root->data) {
        root->left = insertNode(root->left, data);
    } else if (data > root->data) {
        root->right = insertNode(root->right, data);
    }
    // 如果值已经存在，则不插入新节点


    return root;
}

创建二叉树节点的代码如下：

TreeNode* createNode(int data) {
    TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode));
    if (!newNode) {
        printf("Memory allocation failed!\n");
        exit(EXIT_FAILURE);
    }
    newNode->data = data;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

参数data为二叉树节点存储的数据，调用malloc函数为新节点分配内存，将data赋值给新节点的data成员，新节点的left和right成员置为NULL，因为新节点暂时没有左子树和右子树。

树的遍历

树的遍历是依次访问树中的所有节点，即依次对树中每个结点访问一次且仅访问一次。按照节点的访问顺序，遍历算法主要有前序遍历、中序遍历和后序遍历三种方式。

前序遍历：按照根节点->左子树->右子树的顺序进行遍历。具体实现时，先访问根节点，然后递归地遍历左子树，最后递归地遍历右子树。

中序遍历：按照左子树->根节点->右子树的顺序进行遍历。具体实现时，先递归地遍历左子树，然后访问根节点，最后递归地遍历右子树。在二叉搜索树中，中序遍历可以得到一个有序的节点序列。

后序遍历：按照左子树->右子树->根节点的顺序进行遍历。

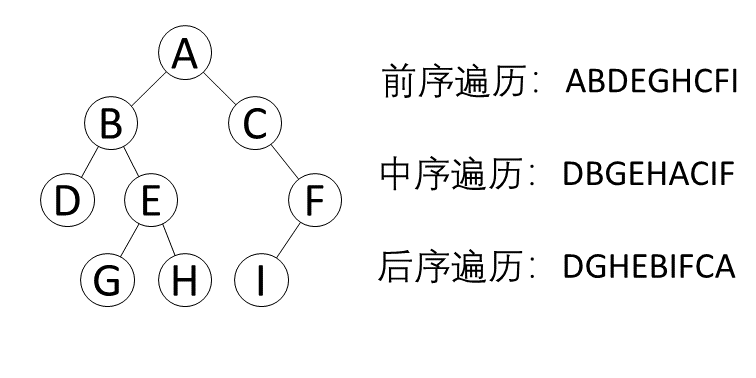
图 1-18树节点不同遍历顺序

以图1-18为例。前序遍历节点访问顺序为ABDEGHCFI，中序遍历节点访问顺序为DBGEHACIF，后序节点的遍历顺序为DGHEBIFCA。

下面给出二叉树前序遍历的递归算法和迭代算法代码，中序遍历和后序遍历由读者给出。

二叉树前序遍历递归代码为：

void preorderTraversal(TreeNode* root) {
    if (root == NULL) {
        return;
    }
    // 访问根节点
    printf("%d ", root->data);


    // 遍历左子树
    preorderTraversal(root->data);


    // 遍历右子树
    preorderTraversal(root->data);
}

preorderTraversal函数采用了递归算法，递归算法是在算法过程中调用自身的算法。递归算法都有一个出口，以结束递归调用。在preorderTraversal函数内，若传入的节点root为空，则结束递归调用，否则输出节点root的数据，然后递归调用preorderTraversal函数，分别遍历左子树和右子树。

前序遍历二叉树也可以采用迭代算法实现：

// 前序遍历的迭代实现
void preorderTraversal(Node* root) {
    if (root == NULL) {
        return;
    }
    // 使用固定大小的栈，实际应用中应使用动态数组或链表
    Node* stack[100];
    int top = -1;
    Node* curr = root;
    while (curr != NULL || top != -1) {
        while (curr != NULL) {
            printf("%d ", curr->data); // 访问当前节点
            stack[++top] = curr;       // 将当前节点压入栈中
            curr = curr->left;         // 移动到左子节点
        }
        if (top != -1) {
            curr = stack[top--];       // 从栈中弹出节点
            curr = curr->right;        // 移动到右子节点
        }
    }
}

在二叉树的遍历过程中，迭代算法的基本思路是借助数据结构（如栈、队列等）来保存待访问的节点信息。

preorderTraversal函数采用栈结构来存储待访问的节点。外层while循环负责遍历树的所有节点，循环条件是节点不为空或者栈不为空，若栈不为空，则从栈内弹出节点，然后将当前节点设置为右子节点；内层while循环输出当前节点信息，并将当前节点压入栈内，然后将当前节点设置为左子节点。

二叉搜索树

二叉搜索树（Binary Search Tree，简称BST），也称为二叉查找树、有序二叉树或排序二叉树。它的左子树上所有节点的值均小于它的根节点的值，而右子树上所有节点的值均大于或等于它的根节点的值；它的左、右子树也分别为二叉搜索树。

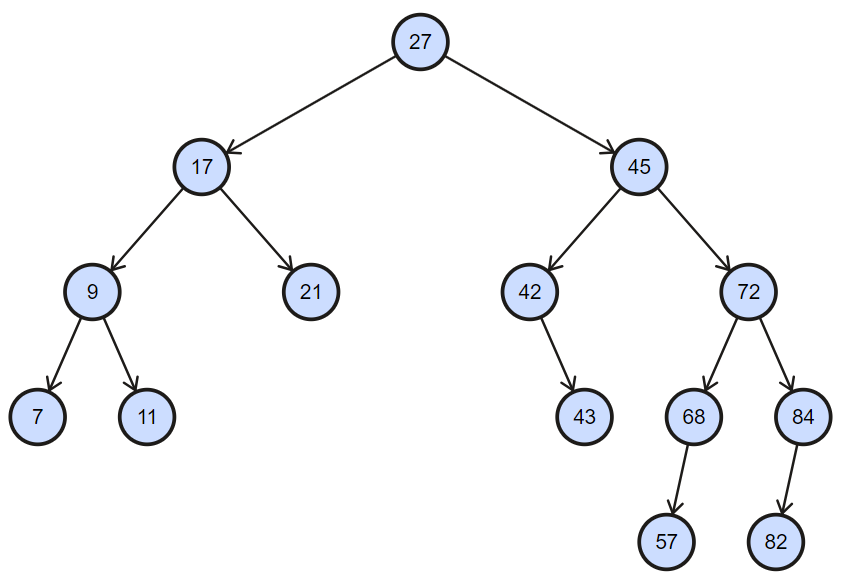
图 1-19二叉搜索树

图1-19为一棵二叉搜索树，根节点左子树所有节点的值都小于根节点，根节点右子树所有节点的值都大于根节点，其子节点遵循同样的规则。

二叉搜索树在查找操作中，即为折半查找。从根节点开始，如果待查找的值小于当前节点的值，则在左子树中继续查找；如果待查找的值大于或等于当前节点的值，则在右子树中继续查找。重复此过程，直到找到目标节点或遍历完整个树。

二叉搜索树插入节点时，首先要执行查找操作，找到待插入值应该插入的位置。如果树为空，则直接创建新节点作为根节点；如果待插入的值小于当前节点的值，则将其插入到左子树中；如果待插入的值大于或等于当前节点的值，则将其插入到右子树中。

二叉搜索树的节点删除操作比较复杂，需要考虑待删除节点的子树情况。如果待删除节点是叶子节点（没有子节点），则直接删除该节点；如果待删除节点只有一个子节点，则将其子节点提升到待删除节点的位置；如果待删除节点有两个子节点，则找到右子树中的最小节点（或左子树中的最大节点）来替换待删除节点，并删除该最小（或最大）节点。

下面是一个简单的C语言程序，用于实现二叉搜索树的插入、查找和删除操作。

#include <stdio.h>
#include <stdlib.h>


// 定义二叉搜索树节点的结构体
typedef struct Node {
    int key;
    struct Node *left, *right;
} Node;


// 创建新节点
Node* newNode(int item) {
    Node* temp = (Node*)malloc(sizeof(Node));
    temp->key = item;
    temp->left = temp->right = NULL;
    return temp;
}


// 插入节点到二叉搜索树
Node* insert(Node* node, int key) {
    // 如果树为空，分配新节点
    if (node == NULL) return newNode(key);


    // 否则，递归下降树
    if (key < node->key)
        node->left  = insert(node->left, key);
    else if (key > node->key)
        node->right = insert(node->right, key);


    // 返回（不变的）节点指针
    return node;
}


// 在二叉搜索树中查找节点
Node* search(Node* root, int key) {
    // 如果树为空或找到键值，返回节点
    if (root == NULL || root->key == key)
        return root;


    // 否则，递归在左或右子树中查找
    if (root->key > key)
        return search(root->left, key);


    return search(root->right, key);
}


// 最小值节点（总是最左边的节点）
Node* minValueNode(Node* node) {
    Node* current = node;


    // 循环直到找到最左边的节点
    while (current->left != NULL)
        current = current->left;


    return current;
}


// 删除节点
Node* deleteNode(Node* root, int key) {
Node *temp,*temp1,*temp2;
    // 如果树为空或未找到键值，返回
    if (root == NULL) return root;


    // 如果键小于根节点的键，则键在左子树中
    if (key < root->key)
        root->left = deleteNode(root->left, key);


    // 如果键大于根节点的键，则键在右子树中
    else if(key > root->key)
        root->right = deleteNode(root->right, key);


    // 如果键与根节点的键相等
    else {
        // 如果节点只有一个子节点或没有子节点
        if (root->left == NULL) {
            temp1 = root->right;
            free(root);
            return temp;
        }
        else if (root->right == NULL) {
            temp2 = root->left;
            free(root);
            return temp;
        }


        // 节点有两个子节点：获取右子树中的最小节点
        temp = minValueNode(root->right);


        // 复制右子树中的最小节点的值到根节点
        root->key = temp->key;


        // 删除右子树中的最小节点
        root->right = deleteNode(root->right, temp->key);
    }


    return root;
}


// 打印中序遍历的结果
void inorder(Node* root) {
    if (root != NULL) {
        inorder(root->left);
        printf("%d ", root->key);
        inorder(root->right);
    }
}


int main() {
    Node* root = NULL;
int i;
int keyToFind;
Node* result;
    int arr[] = {8, 3, 10, 1, 6, 14, 4, 7, 13};
    int n = sizeof(arr)/sizeof(arr[0]);


    // 插入元素到二叉搜索树
    printf("插入元素后的二叉搜索树（中序遍历）: ");
    for (i = 0; i < n; i++)
        root = insert(root, arr[i]);
    inorder(root);
    printf("\n");


    // 查找元素
    keyToFind = 7;
    result = search(root, keyToFind);
    if (result) {
        printf("找到键值 %d\n", keyToFind);
    } else {
        printf("未找到键值 %d\n",keyToFind);
}
}