从“噪”到“净”：Python 高斯滤波

在日常的图像记录与处理过程中，相信许多人都遭遇过类似的困扰，很多拍摄的照片都模糊不清，不知道对这些照片如何处理。今天为大家介绍一个图像处理技术—高斯滤波。我们将通过简单易学的 Python 语言来实现这一技术，即使您是编程领域的初学者，也能够轻松掌握。

高斯滤波的概念

高斯滤波是一种线性平滑滤波器，它通过对图像中的每个像素点及其周围像素点进行加权平均操作，来实现图像的平滑和降噪。
你可以将图像想象成一个由无数小方格组成的大棋盘，每个小方格代表一个像素。当高斯滤波开始工作时，它会以某个像素为中心，给这个中心像素及其周围的像素分配一个“重要程度”，这个“重要程度”在数学上被称为权重。权重的大小取决于像素与中心像素的距离，距离越近的像素权重越大，反之则越小。这种权重分配方式遵循高斯函数分布，因此得名高斯滤波。

具体来说，高斯滤波会按照权重将周围像素的颜色值与中心像素的颜色值进行加权平均，得到一个新的颜色值。这个新的颜色值将替换原来中心像素的颜色值。经过这一番操作，图像中那些因为噪声而显得突兀的像素点就被“平均”掉了，从而使得整个图像变得更加平滑、干净。

高斯滤波的数学原理

高斯函数的图像是一个非常经典的钟形曲线 ，也叫正态分布曲线。

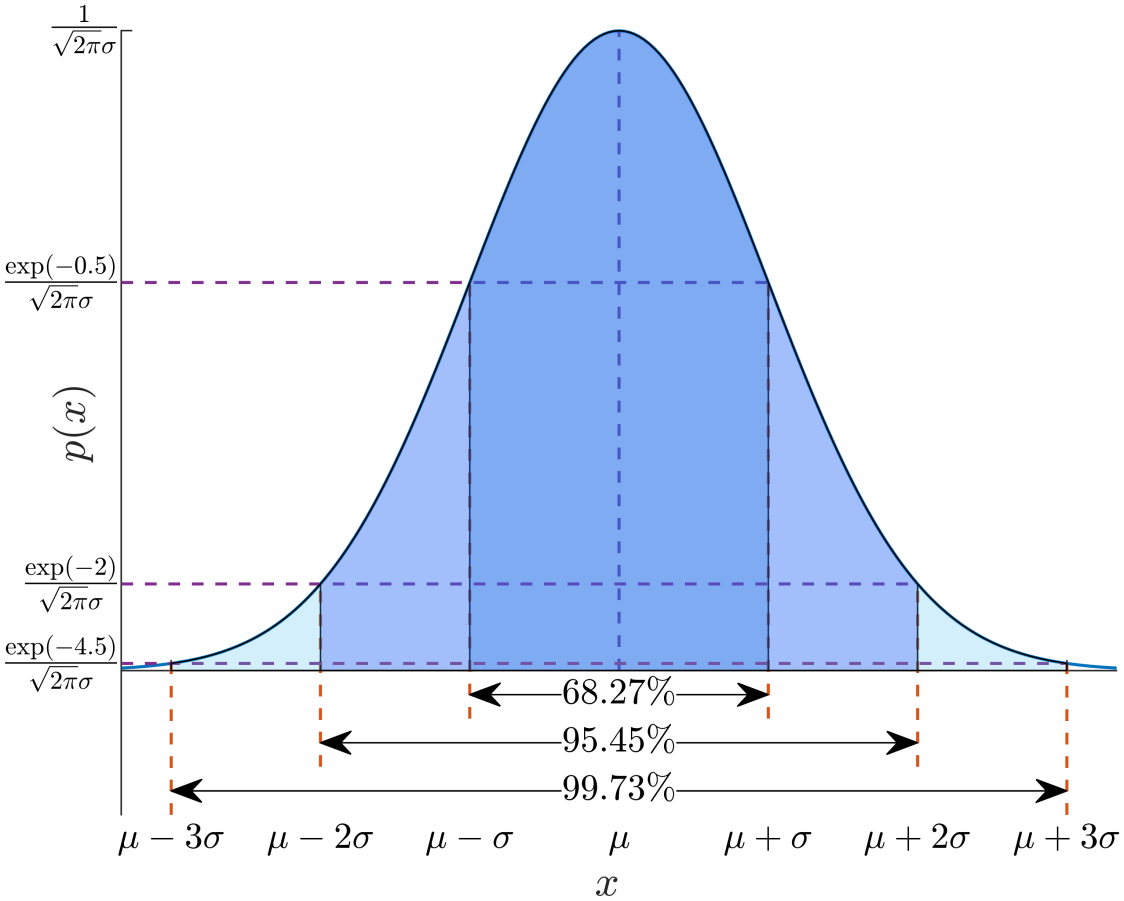
高斯函数（或正态分布曲线）是一种在数学、物理、工程等领域非常常见的概率分布函数。这个函数的曲线形状通常是对称的，像一个钟。我们通过上面的图来了解一下高斯函数的一些关键概念和性质。
（1）平均值（μ）和标准差（σ）‌
图中的曲线是以μ为中心对称的，μ是我们常说的平均值或期望值。σ是标准差，表示数据的离散程度。σ越小，曲线越矮胖；σ越大，曲线越瘦高。
（2）三个重要区域
μ-σ 到μ+σ：这个区间涵盖了大约68.27%的数据点。若多次进行这个分布下的随机抽样，约有68.27%的样本会落在这个区间内。
μ-2σ到μ+ 2σ：这个区间涵盖了大约95.45%的数据点。这说明有95.45%的样本会在这个更宽的区间内。
μ-3σ 到μ+3σ：这个区间涵盖了大约99.73%的数据点。也就是说，几乎所有的样本（99.73%）都会落在这个区间内。
（3）概率密度
图中左侧的p(x)轴表示概率密度。曲线的高低代表了不同x值出现的概率大小。曲线最高的地方就是μ值，代表这里是最可能出现数据点的位置。
（4）积分和概率
曲线下的面积代表了出现的概率。比如，从负无穷到正无穷积分，得到的总面积是1，表示所有可能性加起来是100%。图中标出的三个区域面积分别对应了68.27%、95.45%和99.73%的概率。

在二维平面上，高斯函数的公式：

在这个公式里，(x, y)是像素相对于中心点的坐标， σ 是标准差，它决定了高斯函数的胖瘦，也就是权重的分布范围，e是自然常数。
当我们以某个像素为中心进行高斯滤波时，离这个中心点越近的像素，(x^2 + y^2) 的值就越小，根据高斯函数公式，它对应的权重就越大；反之，离中心点越远的像素，权重就越小。例如在一个(3 X 3)的滤波窗口里，正中间的像素权重最大，而四个角上的像素权重相对较小。这样一来，在计算加权平均值时，中心像素和它附近像素的贡献就更大，从而更好地保留了图像的局部特征，同时又能有效地抑制噪声。
标准差 σ 对高斯滤波的效果有着至关重要的影响。当σ取值较小时，高斯函数的曲线会比较瘦高 ，这意味着只有离中心点很近的像素才会有较大的权重，滤波后的图像会更接近原始图像，保留了更多的细节，但去噪效果相对较弱；而当σ取值较大时，高斯函数的曲线变得矮胖，更多远处的像素也会参与到加权平均中来，图像会变得更加模糊，不过去噪能力也更强。就好像我们调节美颜相机的磨皮强度一样，强度低的时候，能保留面部的一些小细节，比如小雀斑；强度高了，脸就变得超级光滑，连毛孔都看不见了，但同时也可能丢失了一些面部的真实特征。

高斯滤波在 Python 中的实现

了解了高斯滤波的原理后，我们将用 Python 来实现高斯滤波，让模糊的图像变得清晰起来。

准备工作

在开始写代码之前，需要导入两个Python第三方库：OpenCV 和 NumPy 。OpenCV 提供了各种各样的图像处理函数，包括高斯滤波；而NumPy是Python用于科学计算的基础库，它可以高效地处理多维数组，在生成高斯核以及进行卷积运算时，都需要NumPy进行处理。
在 Python 中，导入这两个库的代码非常简单，只需要在文件开头加上以下两行：

import cv2
import numpy as np

编写代码

（1）生成高斯核
要进行高斯滤波，首先得有一个高斯核 。在 OpenCV 中，可以使用cv2.getGaussianKernel函数来生成一维高斯核，然后再通过一些操作将其转换为二维高斯核。下面是生成一个大小为ksize，标准差为sigma的二维高斯核的代码：

def generate_gaussian_kernel(ksize, sigma):
kernel_x = cv2.getGaussianKernel(ksize, sigma)
kernel_y = cv2.getGaussianKernel(ksize, sigma)
kernel = np.dot(kernel_x, kernel_y.T)
return kernel

在这段代码中，cv2.getGaussianKernel函数的第一个参数ksize表示高斯核的大小，必须是奇数，这样才能有一个明确的中心像素；第二个参数sigma就是前面提到的标准差，它决定了高斯核的权重分布。np.dot(kernel_x, kernel_y.T)这一步是将两个一维高斯核进行矩阵乘法，从而得到二维高斯核。
如果想手动生成高斯核，根据前面介绍的高斯函数公式，我们可以编写如下代码：

def manual_generate_gaussian_kernel(ksize, sigma):
kernel = np.zeros((ksize, ksize))
center = ksize // 2
for i in range(ksize):
for j in range(ksize):
x = i - center
y = j - center
kernel[i, j] = (1 / (2 * np.pi * sigma ** 2)) * np.exp(-(x ** 2 + y ** 2) / (2 * sigma ** 2))
kernel = kernel / np.sum(kernel)
return kernel

这段代码通过双重循环遍历高斯核的每个元素，根据高斯函数公式计算出每个位置的权重值，最后再进行归一化处理，确保高斯核所有元素之和为 1。
（2）应用高斯滤波
有了高斯核之后，就可以对图像进行滤波操作了。在 OpenCV 中，有一个非常方便的函数cv2.GaussianBlur，它可以直接对图像应用高斯滤波，一行代码就能搞定：

blurred_image = cv2.GaussianBlur(image, (ksize, ksize), sigma)

这里的image是要处理的图像，(ksize, ksize)是高斯核的大小，sigma是标准差。这个函数会自动生成高斯核，并对图像进行卷积操作，返回滤波后的图像。
如果想自己手动实现高斯滤波，也可以利用前面生成的高斯核，通过卷积操作来实现。卷积操作的原理就是将高斯核与图像的每个像素点及其周围的像素点进行对应元素相乘并求和，从而得到新的像素值。下面是手动实现高斯滤波的代码：

def manual_gaussian_filter(image, kernel):
h, w = image.shape
ksize = kernel.shape[0]
pad = ksize // 2
padded_image = np.pad(image, ((pad, pad), (pad, pad)), mode='constant')
filtered_image = np.zeros_like(image)
for i in range(h):
for j in range(w):
roi = padded_image[i:i + ksize, j:j + ksize]
filtered_image[i, j] = np.sum(roi * kernel)
return filtered_image

在这段代码中，首先对图像进行了边界填充，以确保在卷积过程中不会因为边界像素不足而出现问题。然后通过双重循环遍历图像的每个像素，取出与高斯核大小相同的区域（即感兴趣区域roi），与高斯核进行对应元素相乘并求和，得到滤波后的像素值，最后将所有滤波后的像素值组成新的图像返回。虽然手动实现的过程稍微复杂一些，但能让我们更深入地理解高斯滤波的原理。不过实际应用中，还是推荐使用cv2.GaussianBlur函数，它不仅代码简洁，而且效率更高，经过了优化，能快速处理大规模的图像数据。

完整代码

下面是一个完整的 Python 代码示例，它包含了读取图像、将图像转换为灰度图、应用高斯滤波以及显示图像的全部过程：

import cv2
import numpy as np
import matplotlib.pyplot as plt
# 读取图像
image = cv2.imread('test.jpg')
# 转换为灰度图
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
# 定义高斯核大小和标准差
ksize = 5
sigma = 1.5
# 应用高斯滤波
blurred_image = cv2.GaussianBlur(gray_image, (ksize, ksize), sigma)
# 显示原始图像和滤波后的图像
plt.subplot(1, 2, 1)
plt.imshow(gray_image, cmap='gray')
plt.title('Original Image')
plt.axis('off')
plt.subplot(1, 2, 2)
plt.imshow(blurred_image, cmap='gray')
plt.title('Blurred Image')
plt.axis('off')
plt.show()

在运行这段代码之前，请确保已经安装了 OpenCV 和 Matplotlib 库，并且将test.jpg替换为你自己的图像路径。运行代码后，会弹出一个窗口，显示原始图像和经过高斯滤波后的图像，方便直观地对比效果。