汉诺塔问题

问题描述

汉诺塔（Tower of Hanoi）问题是一个古老的数学难题和经典的递归问题。问题起源于一个古老的传说：有三根柱子，其中一根柱子上自上而下按大小顺序摞着n个不同大小的圆盘，目标是将这些圆盘移动到另外一根柱子上，并满足以下规则：

一次只能移动一个圆盘。
大的圆盘不能叠放在小的圆盘之上。
可以使用第三根柱子作为辅助。

要求用C语言实现汉诺塔问题的解。

解题步骤

解决汉诺塔问题的关键在于理解和应用递归和分治思想。基本的思路是，为了将n个圆盘从起始柱子移动到目标柱子，我们需要先将n-1个较小的圆盘从起始柱子移动到辅助柱子（这本身就是一个汉诺塔问题，但规模较小），然后将最大的圆盘从起始柱子移动到目标柱子，最后再将n-1个圆盘从辅助柱子移动到目标柱子。

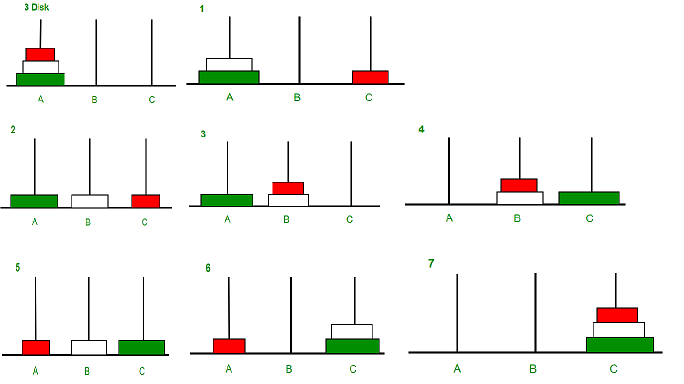
当汉诺塔问题的规模n为3时，意味着有三根柱子（通常命名为A、B、C），并且柱子A上摞着三个按大小顺序排列的圆盘。目标是将这三个圆盘按照规则移动到柱子C上。解题步骤如下：
移动圆盘2和圆盘1到辅助柱子B：

将最小的圆盘（圆盘1）从柱子A移动到柱子C。
将第二小的圆盘（圆盘2）从柱子A移动到柱子B。
将最小的圆盘（圆盘1）从柱子C移动到柱子B，此时辅助柱子B上有两个圆盘，且圆盘1在圆盘2上面。

移动最大的圆盘（圆盘3）到目标柱子C：

将最大的圆盘（圆盘3）从柱子A移动到柱子C。

将圆盘2和圆盘1从辅助柱子B移动到目标柱子C：

将最小的圆盘（圆盘1）从柱子B移动到柱子A。
将第二小的圆盘（圆盘2）从柱子B移动到柱子C。
将最小的圆盘（圆盘1）从柱子A移动到柱子C，此时目标柱子C上有三个圆盘，且按大小顺序排列。

代码实现

#include <stdio.h>

void hanoi(int n, char from, char to, char temp) {
if (n == 1) {
printf("Move disk 1 from %c to %c\n", from, to);
return;
}
hanoi(n - 1, from, temp, to);
printf("Move disk %d from %c to %c\n", n, from, to);
hanoi(n - 1, temp, to, from);
}

int main() {
int n;
printf("Enter the number of disks: ");
scanf("%d", &n);
hanoi(n, 'A', 'C', 'B');
return 0;
}

hanoi 函数是一个递归函数，用于实现汉诺塔问题的核心逻辑。n 表示盘子的数量，from 表示起始柱子，to 表示目标柱子，temp 表示临时柱子。
当 n == 1 时，表示只剩下一个盘子，此时直接将这个盘子从起始柱子移动到目标柱子即可。这是递归的终止条件。
否则，先将 n-1 个盘子从起始柱子移动到临时柱子（以目标柱子作为临时柱子），然后将剩下的一个盘子从起始柱子移动到目标柱子，最后再将 n-1 个盘子从临时柱子移动到目标柱子（以起始柱子作为临时柱子）。这就是汉诺塔问题的递归过程。
在 main 函数中，通过 scanf 函数获取用户输入的盘子数量，然后调用 hanoi 函数开始解决汉诺塔问题。

算法分析

时间复杂度

汉诺塔问题的递归解法的时间复杂度是O(2^n)，其中n是盘子的数量。这是因为每次递归调用都会将问题规模减小1（即n-1），并且每个盘子都需要移动一次。因此，递归树的深度是n，而每一层的操作数是随着递归深度的减小而指数级增长的。具体来说，第一层有1次操作，第二层有2次操作，第三层有4次操作，以此类推，直到第n层有2^(n-1)次操作。因此，总的操作次数是这些层数的操作数之和，即1 + 2 + 4 + ... + 2^(n-1) = 2^n - 1。由于我们只关心最高阶项，所以时间复杂度为O(2^n)。

 

空间复杂度

对于递归函数来说，空间复杂度通常指的是递归调用栈的深度。在这个程序中，递归调用栈的深度也是n，因为每次递归调用都会将问题规模减小1，直到n=1时递归结束。因此，空间复杂度是O(n)。这个空间复杂度并不包括在递归过程中可能创建的其他数据结构（在这个程序中没有创建其他数据结构），只考虑了递归调用栈本身。

对于较大的n值，由于时间复杂度和空间复杂度的指数级增长，可能会导致程序运行缓慢或者栈溢出。在实际应用中，对于大规模的汉诺塔问题，可能需要考虑使用非递归的解法或者优化递归解法来减少时间和空间的消耗。