C语言实现狄克斯特拉算法

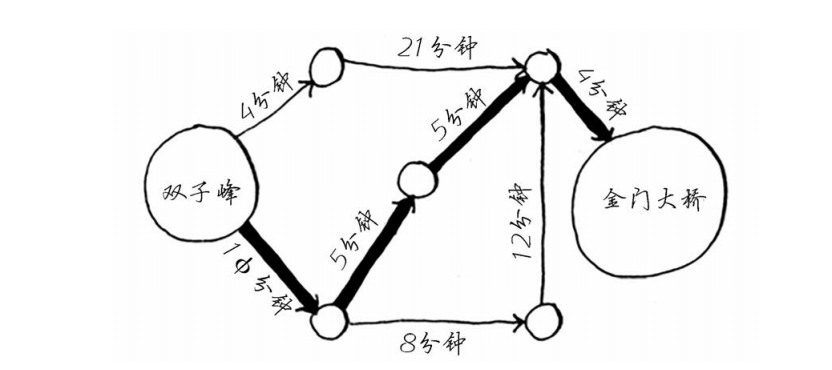
想象一下你站在一个城市的某个地方（起点），想要去城市的其他所有地方（节点），而且你知道每条路（边）的长度（权重）。狄克斯特拉算法就是帮助你找出从你现在站的地方到城市中其他每个地方的最短路径的方法。

狄克斯特拉算法（Dijkstra's algorithm），又称迪杰斯特拉算法，是计算机科学中一种非常重要的算法，它用于在加权图中找到从单一源点到其他所有节点的最短路径。这里的“加权图”指的是图中的每条边都被赋予了一个权重（或者说成本、距离等），这个权重可以是任何实数，但在狄克斯特拉算法中，通常假设这些权重都是非负的。

算法的基本思路

初始化：首先，你把你现在站的地方（起点）到它自己的距离设为0，到其他所有地方的距离都设为无穷大（因为你还不知道怎么去那些地方）。然后，你列出一个待处理的地点列表，里面包含了除了起点以外的所有地方。

逐步扩展：接下来，算法会开始工作。它会在待处理的地点列表中找到一个距离起点最近的地点（注意，这里的“距离”是算法目前认为的最短距离，可能不是真正的最短距离），然后尝试通过这个地点去更新其他地点的最短距离。

更新距离：具体来说，算法会检查刚刚选出的这个地点与哪些地点相连（即存在边），然后计算通过这些边到达那些地点的距离是否比目前算法认为的最短距离还要短。如果是的话，就更新那些地点的最短距离，并记录下是通过哪个地点到达的（这个信息在最后构建最短路径时非常有用）。

重复操作：然后，算法会把这个已经处理过的地点从待处理的地点列表中移除，并继续寻找下一个距离起点最近的地点，重复上述的更新操作。这个过程会一直持续下去，直到待处理的地点列表为空，也就是说，算法已经找到了从起点到所有其他地点的最短路径。

用C语言中实现狄克斯特拉算法，通常需要使用一个优先队列（如最小堆）来高效地选择当前未处理节点中距离最小的节点。为了简化实现，案例将使用一个简单的线性查找加标记已处理节点的方法，这会使算法的时间复杂度提升到O(V^2)（V是顶点数），但在小型图中仍然足够快。

算法案例

以下是一个使用邻接矩阵表示图，并实现了狄克斯特拉算法的C语言示例：

#include <stdio.h>
#include <limits.h> // 用于INT_MAX

#define V 9 // 假设图中有9个顶点

// 用于找到未处理节点中距离最小的节点
int minDistance(int dist[], int sptSet[]) {
int min = INT_MAX, min_index;

for (int v = 0; v < V; v++)
if (sptSet[v] == 0 && dist[v] <= min)
min = dist[v], min_index = v;

return min_index;
}

// 狄克斯特拉算法
void dijkstra(int graph[V][V], int src) {
int dist[V]; // 存储从源点到所有其他点的最短距离
int sptSet[V]; // sptSet[i]为真如果顶点i在最短路径树中或最短距离已确定

// 初始化所有距离为无穷大，sptSet[]为false
for (int i = 0; i < V; i++)
dist[i] = INT_MAX, sptSet[i] = 0;

// 源点到自身的距离总是0
dist[src] = 0;

// 找出所有顶点的最短路径
for (int count = 0; count < V - 1; count++) {
// 选择未处理的节点中距离最小的
int u = minDistance(dist, sptSet);

// 标记当前节点为已处理
sptSet[u] = 1;

// 更新相邻节点的距离
for (int v = 0; v < V; v++)
// 如果v未被处理且存在从u到v的边，则更新dist[v]
if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])
dist[v] = dist[u] + graph[u][v];
}

// 打印计算出的最短距离
printf("Vertex \tDistance from Source\n");
for (int i = 0; i < V; i++)
printf("%d \t\t%d\n", i, dist[i]);
}

// 测试图
int main() {
int graph[V][V] = {{0, 4, 0, 0, 0, 0, 0, 8, 0},
{4, 0, 8, 0, 0, 0, 0, 11, 0},
{0, 8, 0, 7, 0, 4, 0, 0, 2},
{0, 0, 7, 0, 9, 14, 0, 0, 0},
{0, 0, 0, 9, 0, 10, 0, 0, 0},
{0, 0, 4, 14, 10, 0, 2, 0, 0},
{0, 0, 0, 0, 0, 2, 0, 1, 6},
{8, 11, 0, 0, 0, 0, 1, 0, 7},
{0, 0, 2, 0, 0, 0, 6, 7, 0}
};

dijkstra(graph, 0);

return 0;
}

在这个例子中，graph 是一个邻接矩阵，表示图中顶点之间的边和对应的权重。如果顶点 i 和顶点 j 之间没有边，则 graph[i][j] 的值为0。dijkstra 函数实现了狄克斯特拉算法，而 minDistance 函数用于从未处理的节点中找到距离最小的节点。

狄克斯特拉算法非常适用于处理没有负权边的加权图。如果图中存在负权边，那么狄克斯特拉算法就无法正确工作了，因为它总是假设通过当前找到的最短路径到达某个地点的距离是最短的，但在有负权边的情况下，这个假设可能不成立。

此外，狄克斯特拉算法的时间复杂度主要取决于图的边数和节点数，以及算法的具体实现方式。在最坏的情况下，它的时间复杂度可以达到O(n^2)，其中n是节点的数量。但是，通过使用优先队列等数据结构，可以将其时间复杂度降低到O((V+E)logV)，其中V是节点的数量，E是边的数量。