回溯法与经典八皇后问题
- 算法
- 2024-07-05
- 648热度
- 0评论
基本概念
回溯法,其实就是一个“试错”的过程。就像你在解一个复杂的拼图或者迷宫游戏,你会尝试不同的路径,如果发现当前路径走不通,或者不符合条件,你就会退回到上一个分叉点,然后选择另一条路继续尝试。
在编程中,回溯法常用于解决组合问题、搜索问题、决策问题等。它的核心思想是:
定义问题的解空间:这就像是把迷宫的所有可能路径都列出来。
选择搜索策略:决定先尝试哪条路径。比如,你可以从起点开始,每次选择一条没走过的路。
进行剪枝:如果当前路径已经确定不可能达到目标,就及时放弃,不再继续搜索。这就像是在迷宫中,如果你发现前面是堵墙,那你就不会再往前走了。
举个例子,如果你用回溯法解决“八皇后”问题(在8x8的棋盘上放置八个皇后,使得任何一个皇后都不能攻击到其他的皇后,即任意两个皇后都不能处于同一行、同一列或同一斜线上),你会这样操作:
放置第一个皇后在第一行的某一列。
尝试放置第二个皇后在第二行,检查是否与第一个皇后冲突。
如果冲突,就退回第一步,换一列放置第一个皇后。
如果不冲突,继续放置第三个皇后,并检查冲突。
以此类推,直到所有皇后都放置好,或者确定无法放置。
在这个过程中,如果某个皇后放不下,就会退回之前的步骤,重新选择位置。这种不断尝试、不断回溯的过程,就是回溯法的核心。
八皇后问题
问题描述
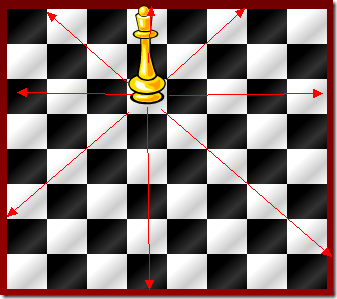
在8×8的国际象棋棋盘上放置八个皇后,使得它们互不攻击。具体地说,就是任意两个皇后都不能处于同一行、同一列或同一斜线上。目标是找出所有可能的摆放方案。
解题步骤
初始化棋盘:创建一个8x8的棋盘,用于表示皇后的位置。可以使用一个一维数组来表示棋盘,其中board[i]表示第i行皇后的列号(0到7)。
定义回溯函数:这个函数将尝试在当前行的每一列放置一个皇后,并递归地调用自身来放置下一行的皇后。
检查冲突:在放置一个皇后之前,需要检查它是否与已放置的皇后冲突。这包括检查同一列、主对角线和副对角线上是否有皇后。
回溯:如果当前位置无法放置皇后(即存在冲突),需要回溯到上一行,并移动那一行的皇后到下一列。
打印解:当成功放置了八个皇后时,打印出当前棋盘的一个解。
主函数:在主函数中,调用回溯函数来开始搜索解空间。
代码实现
#include <stdio.h>
#include <stdbool.h>
#define SIZE 8
int board[SIZE]; // 棋盘,board[i]表示第i行皇后的列号
// 检查是否可以在(row, col)位置放置皇后
bool is_valid(int row, int col) {
for (int i = 0; i < row; i++) {
if (board[i] == col || // 检查列
board[i] - i == col - row || // 检查主对角线
board[i] + i == col + row) { // 检查副对角线
return false;
}
}
return true;
}
// 回溯函数,尝试放置皇后
void place_queen(int row) {
if (row == SIZE) { // 所有皇后都放置完毕,打印棋盘
for (int i = 0; i < SIZE; i++) {
for (int j = 0; j < SIZE; j++) {
printf("%2s", (board[i] == j) ? "Q " : ". ");
}
printf("\n");
}
printf("\n");
return;
}
for (int col = 0; col < SIZE; col++) {
if (is_valid(row, col)) { // 检查当前位置是否可以放置皇后
board[row] = col; // 放置皇后
place_queen(row + 1); // 递归放置下一行的皇后
}
}
}
int main() {
place_queen(0); // 从第一行开始放置皇后
return 0;
}
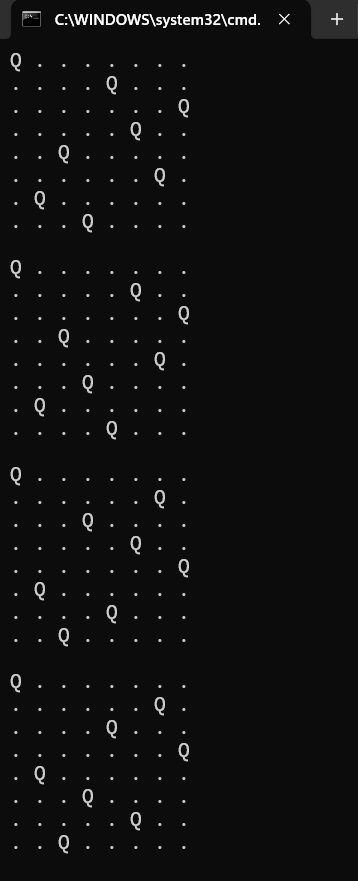
在上面的代码中,is_valid 函数用于检查给定位置是否可以放置皇后,place_queen 函数是一个递归函数,用于尝试在当前行的每一列放置皇后,并递归地调用自身以放置下一行的皇后。当所有皇后都成功放置时,打印出当前的棋盘状态。
算法分析
时间复杂度
八皇后问题中,棋盘的大小是固定的(8x8)。在最坏的情况下,需要检查棋盘上每一个位置是否可以放置皇后。由于棋盘有8行,每一行有8列,所以总共有 8^8 = 16,777,216 种可能的配置。因此,在最坏的情况下,时间复杂度为 O(8^n),其中 n 是棋盘的大小(在这个问题中是8)。
其实实际的执行时间通常会比这个上界要小得多,因为回溯算法会在找到解或确定当前路径不可行时提前停止搜索。因此虽然最坏情况下的时间复杂度很高,但实际运行时间可能要好得多。
空间复杂度
空间复杂度是评估算法执行时所需额外空间的度量。算法使用了一个大小为 SIZE 的数组 board 来存储棋盘的状态,以及几个循环变量和递归调用栈。
数组 board 的大小是固定的(8个整数),因此它的空间需求是常数。循环变量(如 i, j, col)通常也只需要固定大小的内存。
主要的空间开销来自于递归调用栈。在回溯过程中,每一层递归调用都会占用一定的栈空间。由于最多有 SIZE(8)层递归(对应于棋盘的每一行),所以递归调用栈的深度也是常数。
综上所述,该算法的空间复杂度是 O(1),即常数空间复杂度。算法的空间需求不随输入规模的增长而增长。
求解数独
问题描述
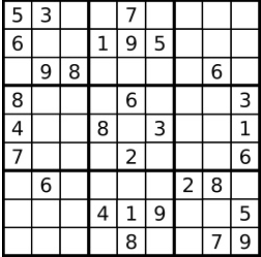
数独(Sūdoku),一种数学游戏。数独的游戏规则是在一个9x9的盘面上,每一行、每一列以及每一个由3x3小格子组成的粗线宫内,都必须包含数字1至9,且每个数字在每一行、每一列和每一个宫内都只能出现一次。游戏开始时,盘面上会给出一些已知的数字作为解题的线索,玩家的目标则是根据这些线索,通过逻辑推理和填数技巧,将剩余空格填满,使得整个盘面满足上述规则。
解题步骤
初始化数独网格:
创建一个9x9的二维数组来代表数独网格。
定义is_valid函数:
此函数用于检查在当前位置(row, col)放置数字num是否有效。
函数遍历当前行、当前列以及当前3x3子网格,检查是否存在与num相同的数字。
如果存在,则返回false,表示放置无效;否则返回true。
定义solveSudoku函数:
这是主要的回溯函数,用于解决数独问题。
它使用两个参数:row和col,表示当前要填充的网格位置。
函数首先检查是否已经遍历完整个网格(即col等于9且row也等于9),如果是,则返回true,表示找到了一个有效的解。
如果当前位置(row, col)已经有数字,则移动到下一个位置(row, col+1)。
如果当前位置为空(即没有数字),则尝试从1到9的数字,看哪个数字可以放置在当前位置。
对于每个尝试的数字,先检查是否有效(使用is_valid函数),如果有效,则放置该数字并递归地尝试下一个位置。
如果递归调用返回true,则表示找到一个有效解,直接返回true。
如果递归调用返回false,则表示当前尝试的数字不合适,需要回溯,即将当前位置的数字置为0,并尝试下一个数字。
如果尝试了1到9的所有数字都不合适,则返回false,表示当前分支无解。
代码实现
#include <stdio.h>
#include <stdbool.h>
#define SIZE 9
void printSudoku(int grid[SIZE][SIZE]) {
for (int i = 0; i < SIZE; i++) {
for (int j = 0; j < SIZE; j++) {
printf("%2d ", grid[i][j]);
}
printf("\n");
if ((i + 1) % 3 == 0) {
printf("-------\n");
}
}
}
bool is_valid(int grid[SIZE][SIZE], int row, int col, int num) {
for (int i = 0; i < SIZE; i++) {
if (grid[row][i] == num) return false; // 检查行
if (grid[i][col] == num) return false; // 检查列
if (grid[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == num) return false; // 检查3x3的宫格
}
return true;
}
bool solveSudoku(int grid[SIZE][SIZE], int row, int col) {
if (row == SIZE) return true; // 所有格子都填完了
if (col == SIZE) { // 当前行填完,填下一行
row++;
col = 0;
}
if (grid[row][col] != 0) { // 当前格子已经有数字了,填下一个格子
return solveSudoku(grid, row, col + 1);
}
for (int num = 1; num <= SIZE; num++) {
if (is_valid(grid, row, col, num)) {
grid[row][col] = num; // 尝试放置数字
if (solveSudoku(grid, row, col + 1)) {
return true; // 递归调用成功,返回true
}
grid[row][col] = 0; // 回溯,尝试下一个数字
}
}
return false; // 尝试完所有数字都不合适,返回false
}
int main() {
int grid[SIZE][SIZE] = {
{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}
};
if (solveSudoku(grid, 0, 0)) {
printSudoku(grid);
} else {
printf("数独无解\n");
}
return 0;
}
is_valid函数用于检查在当前位置(row, col)放置数字num是否有效。solveSudoku函数使用回溯法尝试填充数独网格,并返回是否找到解。
main函数初始化数独网格,并调用solveSudoku函数开始求解。如果找到解,则打印数。
算法分析
时间复杂度
时间复杂度主要取决于搜索树的大小,这取决于数独的填充程度和可能的解的数量。在最坏的情况下,需要尝试所有可能的数字组合,这会导致指数级的时间复杂度。然而,实际的数独问题通常不会达到这种最坏情况,因为有效的剪枝(即is_valid函数的检查)会大大减少需要探索的搜索空间。
空间复杂度
空间复杂度主要由递归调用栈和存储数独网格本身所需的空间决定。由于数独网格是固定大小的(9x9),因此存储网格本身的空间是常数。但递归调用栈的深度取决于搜索树的深度,在复杂的数独问题中,其深度可能会相当大。